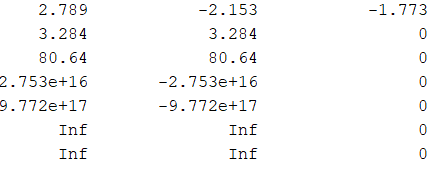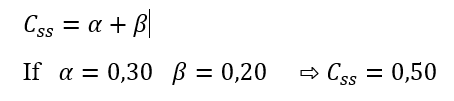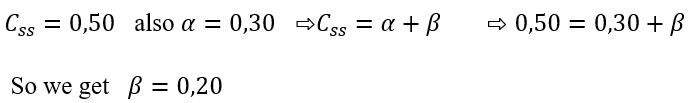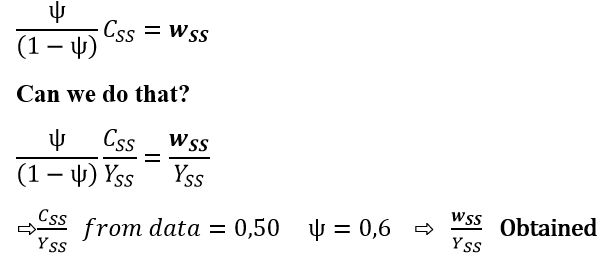My model has 32 equations. I inserted the model linearly into the dynare. To parameterization, I entered the steady state equations of the model into Maple. I entered some parameters such as alpha, beta, etc. also I entered some parameters, such as a_ss/y_ss , b_ss/y_ss and etc from data. And the rest of the parameters were obtained by solving the system of steady state equations in Maple. Of course, when entering the dynare, I did not enter these parameters very accurately.
This is the error that dynare gave me:
STEADY: numerical initial values or parameters incompatible with the following equations
20
Check whether your model is truly linear. Put “resid(1);” before “steady;” to see the problematic equations.
Residuals of the static equations:
Equation number 1 : 0
Equation number 2 : 0
Equation number 3 : 0
Equation number 4 : 0
Equation number 5 : 0
Equation number 6 : 0
Equation number 7 : NaN
Equation number 8 : 0
Equation number 9 : 0.091525
Equation number 10 : 0
Equation number 11 : 0
Equation number 12 : NaN
Equation number 13 : -0.00053773
Equation number 14 : 0
Equation number 15 : 0
Equation number 16 : NaN
Equation number 17 : 0
Equation number 18 : NaN
Equation number 19 : 0
Equation number 20 : NaN
Equation number 21 : 0
Equation number 22 : 0.091525
Equation number 23 : 0
Equation number 24 : 0
Equation number 25 : NaN
Equation number 26 : 0
Equation number 27 : 0
Equation number 28 : 0
Equation number 29 : 0
Equation number 30 : 0
Equation number 31 : 0
Equation number 32 : 0
Error using print_info (line 90)
The steady state contains NaN or Inf
Error in steady (line 104)
print_info(info,options_.noprint, options_);
Error in amirali1 (line 483)
steady;
Error in dynare (line 235)
evalin(‘base’,fname) ;
Is this error because some equations are wrong or Linearization is wrong? Or could it be due to a wrong parameterization?
Dear DoubleBass
Thanks for your reply.I attached the mod amirali1.mod (6.5 KB)
Of course, I have to point out that I did not enter the shock coefficients accurately. I mean, first I wanted to see if the model worked or not, and then if the model answered, I would enter the exact shock coefficients
you have kappa=0; which leads to a division by zero in equation 20. If you parameterize kappa to some value this problem disappears. There is, however, still a problem in your equation 22 that my stem from log-linearization. The first term there (r_ss/(1+pi_ss))*(r-(pi/1+pi_ss)) is not equal to zero. This causes the problem. Maybe you should check your log-linearization. Why do you need the model in log-linear form, you can also put it into Dynare in its non-linear version. Further, there are probably more problems since the Blanchard & Kahn conditions aren’t satisfied.
Dear DoubleBass
many thanks
I set Kappa to a non-zero and that problem was solved. Of course, this error (Blanchard Kahn) appeared later
Using 64-bit preprocessor
Starting Dynare (version 4.5.7).
Starting preprocessing of the model file …
Found 32 equation(s).
Evaluating expressions…done
Computing static model derivatives:
order 1
Computing dynamic model derivatives:
order 1
order 2
Processing outputs …
done
Preprocessing completed.
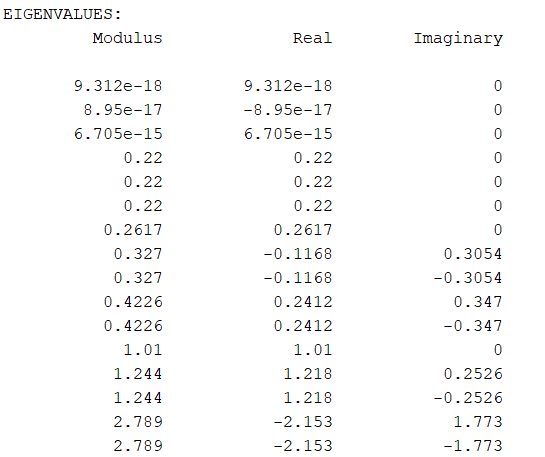
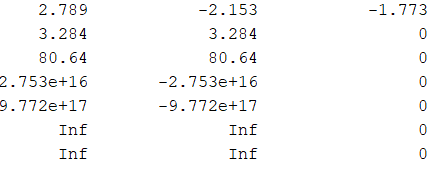
There are 11 eigenvalue(s) larger than 1 in modulus
for 8 forward-looking variable(s)
The rank condition ISN’T verified!
Error using print_info (line 42)
Blanchard Kahn conditions are not satisfied: no stable equilibrium
Error in stoch_simul (line 100)
print_info(info, options_.noprint, options_);
Error in forbearance (line 495)
info = stoch_simul(var_list_);
Error in dynare (line 235)
evalin(‘base’,fname) ;
**Is your suggestion that I enter the model nonlinearly. The problem with this is that my model is a bit large and it is difficult to find the exact variables in steady state.I I attached the model.MODEL.pdf (653.1 KB)
Can this model be solved nonlinearly? Does Maple solve this problem? Or there is a better way? Or continue with the same linear model?**
Since you still have non-zero steady states there is a problem, which is what I meant before. This comes from your equation 22. You can see this by adding resid(1); before the steady command. There is a non-zero residual. As your model is log-linearized all steady states should be zero, thus also the initval block is not needed, but this doesn’t hurt either.
I am not familiar with Maple software, what exactly are you doing there. But since it is possible to log-linearize it there, I do not see a problem giving this to Dynare from the beginnig to do the linearization. It is for sure much less error prone.
The issue with the Blanchard & Kahn conditions could also come from many things, wrong timing, etc. there are countless posts in this forum where you can get an idea what it might be. But right now I would start by making the non-linear version work in Dynare. If you still have problems then it is easier reducing the size to a working version and proceed from there.
Thank you for your warm and timely answer. I have a question about getting variables in the steady state In nonlinear models. What I know in the nonlinear models is that I get the variables as a function of the parameters, for example, the c_ss is a function of alpha beta and … and then I enter the alpha beta and … and get the c_ss accordingly:
For example:
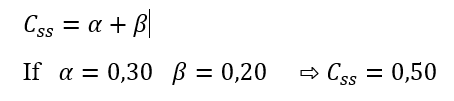
Can parameters be reached from variables?
For example, we know
if this is possible, we can also set some variables in the steady state from the data, and it is only important that our system of equations in the steady state is fully adjusted. That is, we no longer need to obtain all variables as a function of parameters in the steady state. is it correct?
I have another question. Suppose:
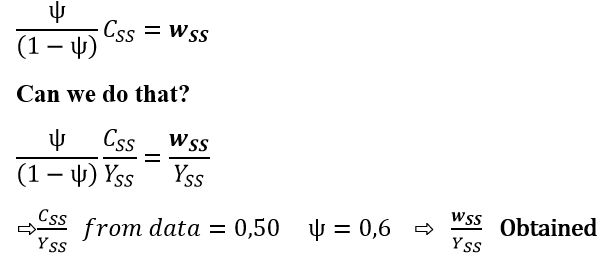
Only our system of equations in the steady state must be perfectly precise and adjustable
If this is true, it will be very easy. And the nonlinear model can be used more easily
Excuse me for taking your time.
many thanks
