Hi everyone,
I’m working on a general equilibrium model with search and matching, featuring two types of workers. I’m solving the model under perfect foresight.
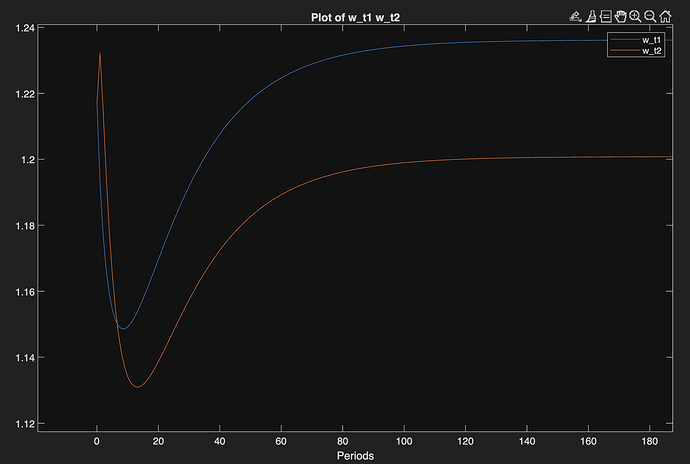
I’m analyzing what happens when there is an exogenous increase in the labor force of type 2 workers. When I simulate this scenario, I observe that the wages for this group (type 2) exhibit overshooting: right after the shock, the wage jumps above its new long-run level and then gradually adjusts downward.
This behavior is illustrated in the attached figure:
What I don’t fully understand is the economic intuition behind this wage overshooting. Could I be modeling something incorrectly, or is there a theoretical explanation for this kind of wage response?
I’ve attached the Dynare codes and a PDF document describing the model’s equations and structure in detail.
I’d really appreciate any insights or suggestions.
Best regards,
Nicolas
model_dynamic.mod (5.4 KB)
solve_SS.m (1.5 KB)
runAll.m (67 Bytes)
stst_guess.mat (1.7 KB)
model_dynamic_steadystate.m (2.1 KB)
example_SM.pdf (121.8 KB)
In period 1, you shock both exogenous shocks. Is that intended? If you don’t shock flow via endval you will see that both wages increase. You need to understand why.
Dear Professor Pfeifer,
Thank you very much for your response.
I realize I wasn’t clear enough regarding the structure of the shocks. The flow shock is meant to determine the increase in labor supply and is included in the endval block. My intention is to indicate that, in the new steady state, the labor force becomes F + flow, and the model should adjust to this new equilibrium accordingly.
The second shock, named tempShock, was introduced for a different purpose. It appears in the equation:
uAcc = (1 - f(-1)) * uAcc(-1) + tempShock;
This variable uAcc is used to model the fact that individuals entering the labor force do not receive unemployment insurance benefits at the begining. As a result, the household’s income from unemployment insurance — defined as z_t2 * u_t2 — does not include these new entrants:
z_t2 * (u_t2 - uAcc)
The dynamics of uAcc are as follows:
uAcc(1) = 0
uAcc(2) = tempShock
uAcc(3) = (1 - f(2)) * uAcc(2)
uAcc(4) = (1 - f(3)) * uAcc(3)
.
.
.
uAcc(N) = (1 - f(N-1)) * uAcc(N - 1) ≈ 0
This sequence captures the idea that the temporary lack of coverage fades gradually over time as these individuals find jobs. I’m not entirely sure if this is the correct way to model it, so I would truly appreciate any remarks or suggestions you may have.
As I wrote, temp_shock alone in period 1 creates an increase in wages. That seems key. The change in flow is insufficient to overturn this.
Thank you Professor Pfeifer, you were right. After removing the parameter, wages behaved as expected. Thanks for the insight.
The issue I’m facing actually comes from a more complex model with two skill levels. I had simplified it earlier to illustrate the problem. In the full version, even when I apply the same flow shock to both types (flow_L and flow_H), one wage still jumps.
A key difference is that Low-skill workers are perfect substitutes, while High-skill labor follows a CES function. I’m not sure if that’s driving the result or if it’s due to calibration.
Thank you in advance.
I’ve attached the updated codes in case it helps clarify the issue:
runAll.m (78 Bytes)
model_dynamic.mod (12.3 KB)
model_dynamic_steadystate.m (3.8 KB)
solve_SS_HL_t1t2.m (3.4 KB)
stst_guess.mat (1.8 KB)