Visualizing / Calculating priors’ PDF

Hi,

I am trying to calculate the pdf of my priors myself and then compare them to the results in oo_.prior_density. Under the Inverse-Gamma distribution my calculations do not always match those of Dynare. Sometime they do, but in some cases they don’t.

Maybe/Hopefully I’m making a stupid mistake (see short code below), but I’d like to see how these are calculated in Dynare.
I’d appreciate directions to code where Dynare calculates the density of the priors.

Many thanks!
Yossi

The prior in the mod file:
Theta2der, inv_gamma_pdf, 7.612968515, 3;
(This implies a mode of 6)

My code for the Inverse-Gamma PDF:
mean = 7.612968515;
var = 3^2;
a = (mean ^2)/var + 2;
b = mean*((mean^2)/var + 1);
ig_pdf = ((b^a)/gamma(a)) .*([0:0.05:15].^(-a-1)) .*exp(-b./[0:0.05:15]);

And the comparison to oo_.prior_density:

image750×467 75.1 KB

Hi,

The priors hyperparameters are calulated in the Dynare function “set_prior”, which is part of the initialization of the estimation in Dynare. Specifically, for the case of Inverse-Gamma distribution, in line 221:
[bayestopt_.p6(k(i)),bayestopt_.p7(k(i))] = inverse_gamma_specification(bayestopt_.p1(k(i)), bayestopt_.p2(k(i))^2, bayestopt_.p3(k(i)), 1, false, bayestopt_.name{k(i)});

The Dynare function “inverse_gamma_specification” description is:
“Computes the inverse Gamma hyperparameters from the prior mean and standard deviation.”

You can debug it to check for the actual calculation for any specific parameters.

Yaakov

Thank you, Yaakov!
This is a step forward. It shows the calculation of the hyper-parameters of the distribution, but I haven’t figured out yet how the pdf itself is calculated. (Which file calls the function inverse_gamma_specification)

It seems Dynare has 2 specifications for the Inverse Gamma distribution, and that in my code I used “type 2” specification. This raises the question how Dynare decides which type to use?

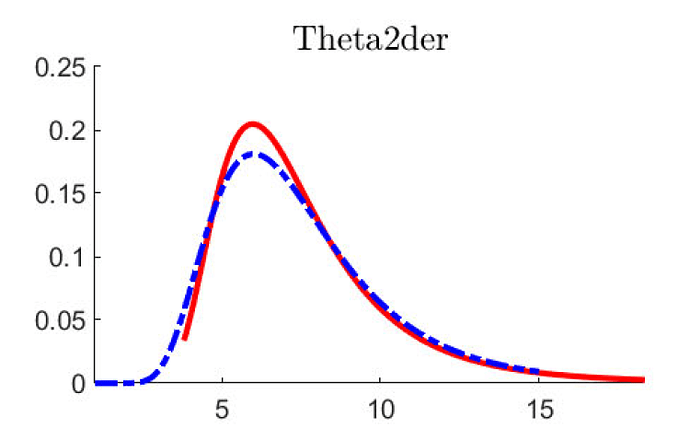
…and also, what generates the difference in the PDFs? (see graph above)

Yossi

Please have a look at

and

Thank you Professor. Much appreciated!

I understand the theoretical part, and of course given the mean and std it does not matter whether we use type I or type II specification.

Nevertheless, I do not understand what is wrong with my calculation (very short code in my first post).

I’d appreciate if you could please direct me to the part in Dynare code that calculates oo_.prior_density. (BTW, I’m using version 5.2)

Can you please provide the full code that generated the graph.

Here it is, together with the mat file containing oo_.prior_density.
The relevant lines are 18-24 and 44-45.

Also please notice that while I chose the prior mean of Theta2der to match a mode of 6 (given std of 3), its value in oo_.prior.mode is slightly off and equals 5.97.

FXI_SOE_NR_EXOGFXest_results_4_ne5.mat (886.6 KB)
Prior_Graphs.m (2.7 KB)

A direct comparison would be

mean_Theta2der = 7.612968515;
var_Theta2der  = 3^2;

x=[0:0.05:15];
[s,nu] = inverse_gamma_specification(mean_Theta2der, var_Theta2der, 0, 1, false, 'Theta');
ldens = log(2) - gammaln(.5*nu) - .5*nu*(log(2)-log(s)) - (nu+1)*log(x) - .5*s./(x.*x) ;

ig_Theta2der_dynare=exp(ldens);

a_Theta2der    = (mean_Theta2der^2)/var_Theta2der + 2;
b_Theta2der    = mean_Theta2der*((mean_Theta2der^2)/var_Theta2der + 1);
ig_Theta2der   = ((b_Theta2der^a_Theta2der)/gamma(a_Theta2der))...
                 .*([0:0.05:15].^(-a_Theta2der-1))...
                 .*exp(-b_Theta2der./[0:0.05:15]);

plot(x,ig_Theta2der)
hold on
plot(x,ig_Theta2der_dynare)

So it seems you are working with a different distribution/parameterization than Dynare.

Thanks! I got it now. The pdf in Dynare is:

PDF\left( x\right) =\frac{\left( \frac{s}{2}\right) ^{\frac{1}{2}}}{\Gamma \left( \frac{\nu }{2}\right) }\left( x^{2}\right) ^{-\left( \frac{\nu }{2} +1\right) }\exp \left( -\frac{s}{2x^{2}}\right) \times 2x^{\frac{1}{2}}

This means that x^2 is inverse Gamma, not x (In the sense that \frac{1}{x^2} follows the Gamma distribution, \frac{1}{x} does not).

So my understanding is that when setting the prior I should have called inv_gamma2_pdf, not inv_gamma_pdf, as the latter calls inv_gamma1_pdf by default. inv_gamma1_pdf is suitable for estimating standard errors when assuming the variance is Inverse Gamma.
Hope this is correct…

Many thanks!
Yossi

Yes, that makes sense.