Simulating Long-Run Risk Model

General DSGE Modeling Replication Attempts
1

I am trying to simulate the Bansal/Yaron (2004) long-run risk model, and have it set up with their equations and parameter values. Although the model is simulated at monthly frequency, according to them the simulations should imply an annualized first-order autocorrelation of consumption of around .49. Yet when I simulate it using the code below, consumption has a first-order autocorrelation of only .03. I’d be really grateful if anyone could perhaps suggest where I am going wrong. Thanks.

var x y vol rf ;
varexo e_x e_u e_v ;

parameters rho sigma_x mu_y mu_v v sigma_v ;

mu_y = 0.0015;
rho = 0.979;
sigma_x = .044;
mu_v = 0.00788;
v = 0.987;
sigma_v = 0.0000023;
phi=3;

model;
x=rhox(-1) + sigma_xvol(-1)e_x;
y=mu_y + x(-1) + vol(-1)e_u;
vol^2=mu_v^2+v(vol(-1)^2-mu_v^2)+sigma_ve_v;

(1+y(+1))^(-1/2)(1+rf).99=1;
end;

initval;
x=0;
y=mu_y;
vol=mu_v;
end;

steady;

shocks;
var e_x;
stderr 1;
var e_u;
stderr 1;
var e_v;
stderr 1;
var e_d;
stderr 1;
end;

stoch_simul(periods=15000, drop=100, irf=30, order=3, pruning, nograph);

2

It is hard to follow which case and which equations you actually implemented. Could you please add the information to the mod-file using comments. Also, what is the hard-coded 0.99?

3

I have the same problem. Can you explain me why? I am attaching my mod file
growth.mod (976 Bytes)

4

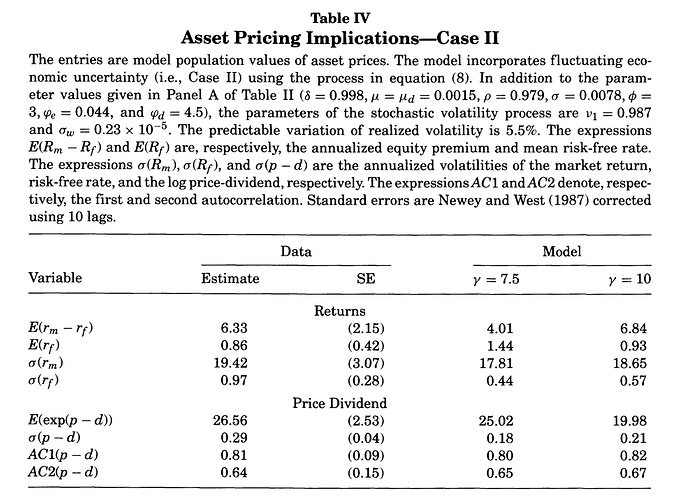
It should be along the lines of

// Variables and Parameters
var         
    g 
    g_d
    x
;

varexo ec
    ex
    ed
;

parameters  mu mu_d phi rho phi_d phi_e siggma;



mu = 0.0015;            // Long run mean of consumption growth
mu_d = 0.0015;            // Long run mean of consumption growth
rho = 0.979;            // Persistence of long run shock
siggma=0.0078;
phi = 3;            // Aggregate dividend loading on LRR
phi_e=0.044;
phi_d=4.5;

// Model
model;
// Exogenuous processes
x = rho*x(-1)+phi_e*siggma*ex;
g = mu+x(-1)+siggma*ec;
g_d = mu_d+phi*x(-1)+phi_d*siggma*ed;

end;

// Initital Values
initval;
x = 0;
g = mu;
g_d = mu;
end;

shocks;
var ec=1;
var ex=1;
var ed=1;
end;

stoch_simul(order=1,periods=840,simul_replic=1000);
[simulated_series]=get_simul_replications(M_,options_);


%% get info about dimensions
replications=size(simulated_series,3);
n_years=floor(size(simulated_series,2)/12);

g_annual=NaN(replications,n_years);
%g_annual_geo=NaN(replications,n_years);
g_d_annual=NaN(replications,n_years);

for ii=1:n_years
    g_annual(:,ii)=squeeze(sum(simulated_series(strmatch('g',M_.endo_names,'exact'),(ii-1)*12+1:ii*12,:)));
    %g_annual_geo(:,ii)=squeeze(prod(1+simulated_series(strmatch('g',M_.endo_names,'exact'),(ii-1)*12+1:ii*12,:),2))-1;

    g_d_annual(:,ii)=squeeze(sum(simulated_series(strmatch('g_d',M_.endo_names,'exact'),(ii-1)*12+1:ii*12,:)));
end

g_std=std(g_annual,0,2);
%g_std_geo=std(g_annual_geo,0,2);
g_autocorr=NaN(replications,1+10);
for ii=1:replications
    g_autocorr(ii,:)=autocorr(g_annual(ii,:),10);
end
g_autocorr(:,1)=[]; %remove 0th autocorrelation
mean(g_autocorr)
quantile(g_autocorr,[0.95,0.05])

mean(g_std)
quantile(g_std,[0.95,0.05])
g_d_std=std(g_d_annual,0,2);
mean(g_d_std)
quantile(g_d_std,[0.95,0.05])
g_d_autocorr=NaN(replications,1+1);
for ii=1:replications
    g_d_autocorr(ii,:)=autocorr(g_d_annual(ii,:),1);
end
g_d_autocorr(:,1)=[]; %remove 0th autocorrelation
mean(g_d_autocorr)
quantile(g_d_autocorr,[0.95,0.05])


corr_g_g_d=diag(corr(g_annual',g_d_annual'));
mean(corr_g_g_d)
quantile(corr_g_g_d,[0.95,0.05])

but the overall results do not perfectly fit. You will need the file at DSGE_mod/Hansen_1985 at master · JohannesPfeifer/DSGE_mod · GitHub

8

fst.mod (3.5 KB)

Screenshot 2023-04-07 151404
Screenshot 2023-04-07 151404976×716 90.2 KB

I have this.
Note: numbers do not add up to 100 due to i) non-zero correlation of simulated shocks in small samples and ii) nonlinearity

Unable to perform assignment because the size of the left side is 1-by-1 and the size of the right side
is 1000-by-1.

Error in fst.driver (line 317)
g_annual(:,ii)=squeeze(sum(simulated_series(strmatch(‘g’,M_.endo_names,‘exact’),(ii-1)12+1:ii12,:)));

Error in dynare (line 278)
evalin(‘base’,[fname ‘.driver’]);

9

It must be

replications=size(simulated_series,3);

not

replications=size(simulated_series,4);
10

The problem i have when i consider order 3 (since in BY2004 I have stochastic volatility) is the following ones
fst.mod (3.6 KB)

dynare_simul_ must have at least 12 input parameters and exactly 2 output arguments.

Error using reshape
Number of elements must not change. Use [] as one of the size inputs to automatically calculate the
appropriate size for that dimension.

Error in get_simul_replications (line 41)
sim_array=reshape(simulations,[M_.endo_nbr options_.periods options_.simul_replic]);

Error in fst.driver (line 312)
[simulated_series]=get_simul_replications(M_,options_);

Error in dynare (line 278)
evalin(‘base’,[fname ‘.driver’]);

11

Are you using Dynare 5.4?

12

Yes

13

But for some reason, there must be a version conflict given the message

dynare_simul_ must have at least 12 input parameters and exactly 2 output arguments

14

In the matlab folder there is no file called dynare_simul_. Is this a possibile reason?

15

There should be a mex-file.

16

I fix it. Thank you. The problem is that I cannot still match the simulated moments by a lot from the table above. Am i still doing something wrong? Are the equations wrong?
fst.mod (3.9 KB)
(in excret_annual i have in the first year -6 which makes nosense)

17

That is hard to tell. Have other papers replicated the original numbers. It’s striking that already the numbers for the exogenous processes are quite off. Also note that Barrilas et al’s “Practicing Dynare” contained the Bansal/Yaron model, see Practicing Dynare_2019(updated version)
But I don’t know whether that one was correct either.