Hello everyone,
I have a problem when trying to run my .mod file performing a second order approximation. When I simulate the model at first order everything goes right and I get the corresponding IRFs. But as I want to get Welfare values I need to simulate the model at second order and then I get the error message:
stoch_simul:: The simulations conducted for generating IRFs to epssigma were explosive.
stoch_simul:: No IRFs will be displayed. Either reduce the shock size,
stoch_simul:: use pruning, or set the approximation order to 1.
If I reduce the shock size my Welfare values change. So I try to use pruning but then I get very weird IRFs, that follow the same path as when I simulate at first order approximation but with a los of fluctuations:
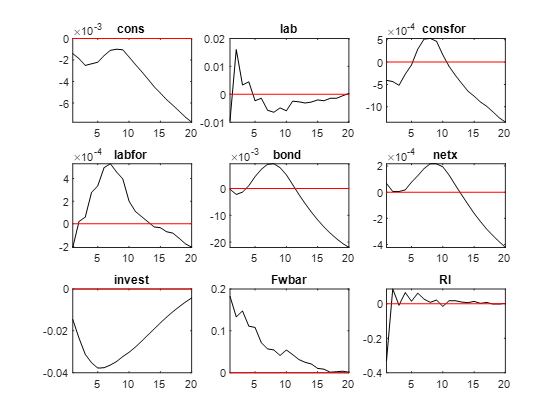
Can someone tell me why I have these results?
Thank you very much for your help!
M
If the object of interest for you is the stochastic (ergodic) mean of welfare, it might be the case that you are not interested in the graphical visualisation of IRFs, as most often it is the case. Therefore, you only need to solve the model at second-order and switch IRFs off. For ergodicity, you also need many replications, say 1000.
If you are interested in the graphical visualisation of IRFs, then pruning and reducing the size of the shock are both viable options, provided that one bears in mind that shock size matters in a second-order approximation due to the absence of certainty equivalence. Personally, I believe reducing the shock size is a slightly poorer substitute for pruning, especially if you have an estimated shock size that you are reluctant to change.
If you produce enough replications, say 1000, the simulated IRFs (higher-order IRFs are called GIRFs because they are state-dependent) will not be lumpy.
Try
stoch_simul(order=2,irf=0, replic=1000);
You can always increase the number of replications to make GIRFs smoother.
Thank you very much for your answer cmarch. The problem is that I need the graphical visualisation of the IRFs because I am interested in obtaining both the mean of welfare and its graphical response to the shock. However if I use as you propose
stoch_simul(order=2,irf=0, replic=1000);
then I get no graphical visualisation at all. If I try with
stoch_simul(order=2,irf=20, replic=1000);
then I get the same error that I got at the begining.
stoch_simul:: The simulations conducted for generating IRFs to epssigma were explosive.
stoch_simul:: No IRFs will be displayed. Either reduce the shock size,
stoch_simul:: use pruning, or set the approximation order to 1.
So I believe that the only option that I have is to reduce the shock size considering that the IRFs are also lumpy with pruning, right?
Not really. As mentioned in the previous post, you can use pruning in substitution for changing your shock size
Also, increase the number of replications.
This issue is a bit more complicated. @cmarch is correct that you need a high number of repetitions to get smooth IRFs. But that does not help when simulations are explosive.
The problem is that both options, reducing the shock size and pruning are unattractive options. As the model is nonlinear, the shock size matters, so using a smaller one will give different results.
Pruning implies using an augmented state space, so the model is different the non-pruned model, which will drive results as well. My impression is that of the two unattractive choices pruning is the most common one.
Thank you jpfeifer. The problem is that pruning does not solve the issue of the lumpy IRFs. I can only get smooth IRFs by reducing the shock size (but my results change) or by runing around 10.000 replications (but it gets around an hour and I need to run a lot of codes… and the IRFs also change slightly).
Could I do it in two steps? First use stoch_simul(order=2,irf=0); to get the Welfare values and secondly use stoch_simul(order=1,irf=20); to get the IRFs?
So can I reduce the shock size by dividing it by 100, for instance, in order to get the IRFs and then multiply those IRFs by 100? Would the results be correct?
