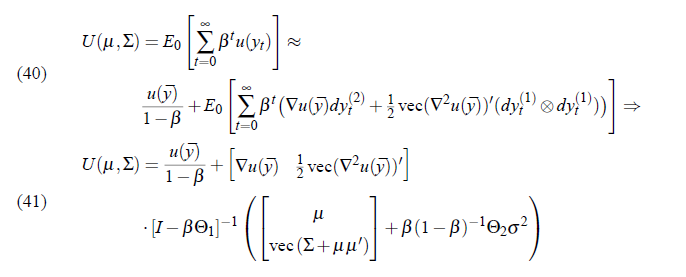Hi everyone,
I’m looking to calculate welfare, defined as the discounted sum of expected utility conditional on the steady state as the initial condition. This would be straightforward, except that period utility has a unit root thus the unconditional moments don’t exist and DYNARE excludes this variable when solving the Lyapunov equations. However, the conditional moments exist and should be computable. The paper by Kim, Kim, Schaumberg and Sims suggest that conditional welfare as defined should be given by the following equation (40 and 41 in the paper). Has anyone tried calculating this, given that DYNARE already makes use of this paper for its second order approximation with pruning?
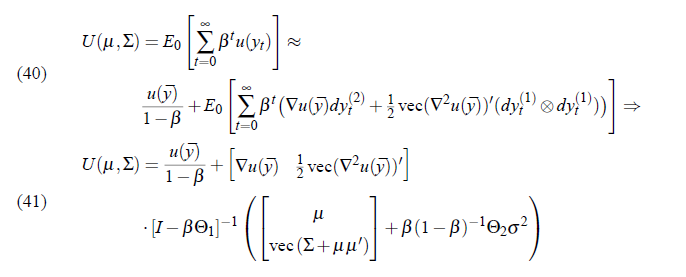
The unit root also means that simulating and taking an average also will not work which seems to be the suggestion in Second order approximation and pruning
If anyone can be of any help, this will be much appreciated,
All the best,
Tim
Dynare never provides a conditional moment in its default output. But you can easily compute it along the lines of :https://github.com/JohannesPfeifer/DSGE_mod/blob/master/Born_Pfeifer_2018/Welfare/get_consumption_equivalent_conditional_welfare.m
%% simulate conditional welfare
initial_condition_states = repmat(oo_.dr.ys,1,M_.maximum_lag); %get steady state as initial condition
shock_matrix = zeros(1,M_.exo_nbr); %create shock matrix with number of time periods in rows
y_sim = simult_(initial_condition_states,oo_.dr,shock_matrix,options_.order); %simulate one period to get value
outvalue=y_sim(strmatch('Welfare_gap',M_.endo_names,'exact'),2)*100; %read out gap
Dear Johannes,
Thank you, I came across this code in an earlier post of yours. Using the notation in the DYNARE manual, I believe the output of your code gives y^s + 0.5 \Delta^2 and I see that Schmitt-Gruhe and Uribe refer to this as the conditional moment. It’s not immediately clear to me how the second term of this expression is equivalent to the second term in the Kim, Kim, Schaumberg and Sims expression I posted – are these the same or am I not comparing like with like?
Thanks for your help,
Tim
The formula you posted shows how to compute welfare from the felicity function u() and the solution for the variables dy. In my code welfare is directly computed together with the dy as it is treated as a regular variable.
Ah I see, yes that makes sense. Thanks.