Help! The replicate of Christensen and Dib (2008)

General DSGE Modeling Replication Attempts
1

Hello :slightly_smiling_face:, I am trying to replicate a simplified version of Christensen and Dib (2008), and I believe I had done it as accurately as I could.

But a problem is: when I increase the financial accelerator parameter β€œu” (which determines whether there is financial accelerator), the IRFs of monertary shock become more stable, which go against result of the Christensen and Dib (2008). Can someone tell me why and how to fix it :sob:?

I guess the reason may be this: My model is nolinear. It means when β€œu” is increased, the calibrated steady state of some other variable is also changed. Then this variable’s changed steady state will work against β€œu” 's accelerator effect and make the model more stable to shocks.
Maybe this is why there is only linear code of Christensen and Dib (2008) (as in linear version, the steady states of variables is all zero, and will not be affected by paremeters):thinking:.

Below is my code and model, Please help :rose:!
model.pdf (76.0 KB)
BGG_myself_log_form.mod (4.2 KB)
test_of_FA.m (1.3 KB)
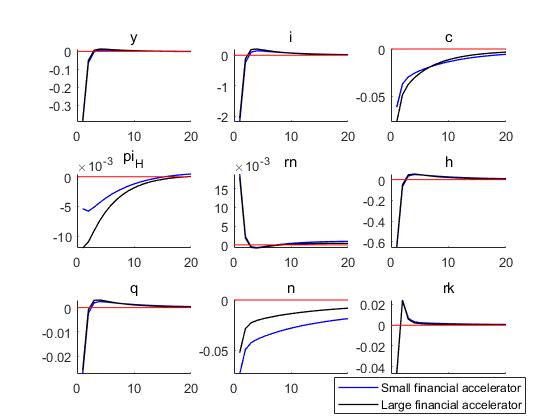
You can directly run the test_of_FA.m to get the follow result. As you can see, when u is larger, output, net worth and other variables become more stable, but cosumption becomes more fluctuant.

Many thanks for your help!

Zhang Zhanpei
untitled

1 Like
2

A couple of years ago, some students of mine tried to replicate the paper and failed as well. Calibration of the nonlinear version seems close to impossible.

1 Like
3

Thanks for your reply, Professor jpfeifer. Do you know what causes this problem? Is it the reason I mentioned above?

4

I am attaching some of the findings, although I have not verified them.
CD.pdf (224.9 KB)
Let me know whether it makes sense.

5

Thanks, Professor jpfeifer. It seems the key difference between your pdf and mine are the setting of external finance premium function. In your model, you let

图片
图片1010Γ—90 8.27 KB

while in my model, I set 图片.
I am sure in my setting, the condition 图片 holds. But I am not sure if this condition holds in your setting (as this is a quadratic function). Maybe it is this distinction brings different results between our models. I will keep looking.

Thanks again, Professor.

Zhang Zhanpei