Why is sensitivity analysis for phi_pi different across models

Identification/Sensitivity
1

I expected sensitivity analysis for phy_pi in the Taylor rule to be similar across models, but it seems that is not the case.

  1. I added the following to Gali_2015_chapter_4.mod
varobs pi y_gap y_nat y yhat r_nat r_real i n m_real m_growth_ann nu a r_real_ann i_ann r_nat_ann pi_ann z;
estimated_params;
phi_pi, 1.5, 0, 2;
phi_y, 0.125, 0, 2;
end;
dynare_sensitivity;

Which gave me indeterminacy and unique Single Saddle-Path graphs

ch4
ch42

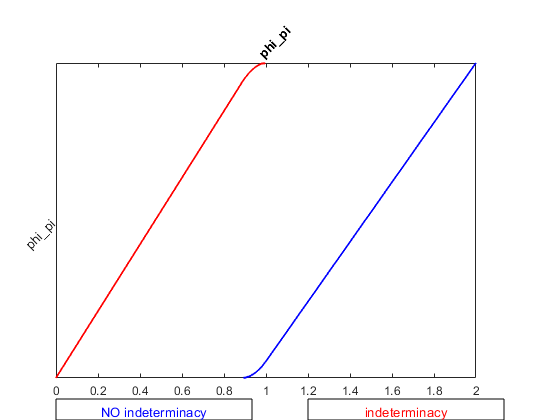
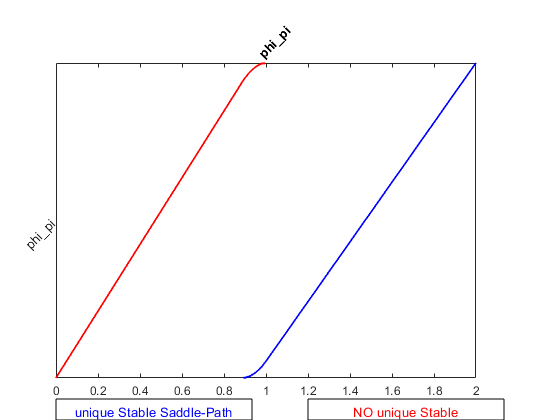
  1. Then I added the following to Gali_2015_chapter_6.mod
varobs pi_p y_gap y_nat y yhat r_nat r_real i n m_real m_growth_ann m_nominal nu a r_real_ann i_ann r_nat_ann pi_p_ann z p w c w_real w_gap pi_w w_nat mu_p pi_w_ann;
estimated_params;
phi_pi, 1.5, 0, 2;
phi_y, 0.125, 0, 2;
end;
dynare_sensitivity;

Which gave me explosive solution and unique Single Saddle-Path graphs

ch6
ch62

QUESTIONS
a. Why does phy_y appear in (2) and not (1)?
b. And why does indeterminacy in the little box below the graph change to explosive solution? I know indeterminacy means explosive solution, but just curious about the different names used.
c. I am also confused about the interpretation in (2). In (1), the graph shows **phy_pi ** should be more than 1 (approximately) to ensure a unique solution, and the blue line is at the right of the red line. Why is it that in (2), the blue line is at the left of the red line instead? How to interpret it? It seems **phy_pi ** should be less than 1 (approximately) to ensure a unique solution, which can not be.

  1. Lastly, I added the following to Gali_2015_chapter_8.mod
varobs y_gap pi_h i y_nat r_nat s_nat y s_gap s pi n r_real w nx c yhat p_h p er d_er y_star a nu z r_real_ann i_ann r_nat_ann pi_ann pi_h_ann;
estimated_params;
phi_pi, 1.5, 0, 2;
phi_y, 0.125, 0, 2;
end;
dynare_sensitivity;

Which gave me no graphs but

 0.0% of the prior support gives unique saddle-path solution.
100.0% of the prior support gives explosive dynamics.
All parameter values in the specified ranges are not acceptable!
Sensitivity computations stopped: no parameter set provided a unique solution
Total computing time : 0h00m35s

QUESTIONS
If 100.0% of the prior support (I guess from 0 to 2) gives explosive dynamics, why do I not have ‘The rank condition isn’t verified’ error when I set phi_pi = 1.5 and phi_y = 0.125 in the model?

Sorry for such a long post.

2

  1. Because for the simple model, only inflation feedback is relevant. However, once you add wage rigidity, that changes and output feedback becomes relevant as well.

  2. Those are two different concepts. Instability/explosiveness means that no bounded solution exists as variables explode. Indeterminacy means there are many solutions and nothing tells you which one you should pick. Those are two instances for which the Blanchard-Kahn conditions can be violated.

The model has a unit root and you did not set diffuse_filter. That screws up the graphs and also is the problem for Gali_2015_chapter_8.mod

1 Like