I am unable to figure out why “EVEN” a large shock to monetary policy leads to a very small increase (not even 5 basis points) in the policy interest rate in my model. Can anyone figure out what is the arithmetic.
Thanks
Steve
slov_jul5_1536.mod (8.3 KB)
1 Like
Because there is a feedback mechanism in your monetary policy equation. If you shut down y and pi in the equation: 1+r = (1+r_bar)^phir * (1 + r(-1))^(1-phir) * (1/pi_bar)^((1-phir)*neta)*(1/y_bar)^((1-phir)*zeta)*epsm;, and assume the following
var epsmss;
stderr 0.01;
Then you have this graph.
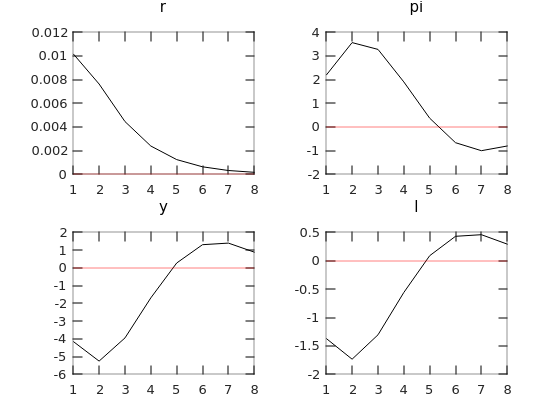
Of course, there is feedback from y to r in every Taylor rule, but the reason why r only rises a little in the original model you sent is that y falls too much, which is a result of the parameters in the model. Because there is feedback from y to r in equation //Central Bank (34), r can even be negative after a contractionary monetary policy shock depending on the parameters in the model. That is, if y falls too much, r can rise only a little or can even be negative.
By the way, maybe inflation should be falling too since this a contractionary monetary policy…
On the right size of a shock, sometimes it depends on what you want the IRFs to be. But normally, they are 0.01. You can change the size of a shock to match say IRFs of an SVAR model.
Actually when I partially shut off y by reducing the coefficient on output gap in the taylor rule, the rate of interest hardly rises (rather it is flat). In words, if the central bank attaches a higher weightage to inflation stabilisation than output stabilisation, output gaps may rise in the future and this spikes inflation today as inflation is a function of future inflation and future path of output gaps through NKPC. So I believe it is not taylor rule alone which explains the pass through of monetary policy shock to interest rates and inflation. NKPC plays a big role…
Yeah, maybe. I was, however, pointing to the fact that given i_t = \rho + \psi_{\pi}\bar{\pi_t} +\psi_{y}\bar{y_t} + e_t, for example, i_t could fall even after a contractionary monetary policy shock depending on your model and how it is calibrated, which determines how y_t and \pi_t reacts.
That is precisely the point. What is the guidance on parameters. Shutting off y, as you are suggesting is not a solution.
What parameters to use? The answer typically is, it depends on your goal. For example, if you want to compare your model to other models already in the literature, you can use parameters in other studies…those studies you want to compare your paper with.
Parameters can come from microdata… Willi Mutschler warns on aggregation issues.
You can calibrate your model to target some big ratios like C/L, etc. More info here on calibration:
Read also open economy macroeconomics by M. Uribe and S. Schmitt-Grohé. They talk about calibrating
(a) Parameters Based On Sources Unrelated To The Data The Model Aims To
Explain
(b) Parameters Set To Match First Moments Of The Data The Model Aims To
Explain
(c) Parameters Set To Match Second Moments Of The Data The Model Aims
To Explain
You can start here but you can find hints on calibration in several other places. If you calibrate your model based on your goal and interest rate responds little to contractionary monetary policyshock, then I guess it is a structural feature of the model, and maybe consider modifying the structural features of the model, not only parameters.
Thank you Professor @jpfeifer!
Is there a document/notes that explains this link with NKPC clearly, particularly what you explained.
Galí’s textbook shows the analytical solution to the basic New Keynesian model. You can see there how the various parameters of the model affect the solution.

