In DSGE-VAR in dynare, what is the identification strategy (of the structural shocks) of the VAR part? Cholesky decomposition?
I was reading one paper where they simulate data from DSGE and apply VAR to the simulated data where structural shocks in the VAR are identified via a recursive ordering. The VAR IRFs (orderings 1 and 2) below are nowhere close to the DSGE IRFs (True) irrespective of the recursive structure of the VAR. They advise using sign restrictions for VARs. Should the VAR part of DSGE-VAR use sign restrictions too?
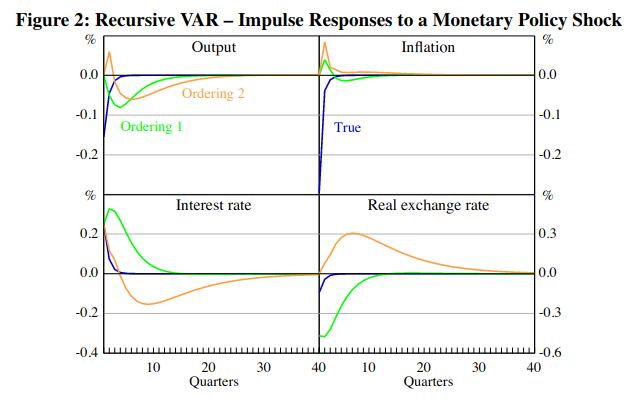
My problem: I am trying to study how a given set of shocks propagates through some economy A…but I am skeptical about using any VAR/SVAR model for economy A as ‘evidence’ as that evidence seems to be subjective.
Maybe choose restrictions such that VAR results match conventional wisdom? For example, in Gali’s book, he presents SVAR results from CEE(1999) as evidence of monetary policy transmission mechanism under a specific ordering of the variables in the SVAR. But this ‘evidence’ is subjective, right? I guess if CEE’s SVAR model violates conventional wisdom using data of some other country A, then one must change the restrictions until the VAR model for country A matches conventional wisdom (which is sort of based on theory)? But if that is the case, then why do we need to use a restricted VAR/SVAR model in the first place as evidence to validate a DSGE model?
I am kind of struggling with these thoughts. Like we can validate DSGE with VAR, but the VAR isn’t perfect either and we may need to put restrictions to match conventional wisdom. But conventional wisdom is based on the theory it seems…Any comments would be very much appreciated.
Hi Emmanuel,
I will assume you DSGE model has a VAR representation.
For a given parametrization \theta, your DSGE model has its own identification scheme:
D(\theta)=\Sigma^{*}(\theta) \Omega^{*}(\theta)
where D is the impact matrix mapping the structural shocks to the forecast errors in the data, \Sigma is the the Cholesky decomposition of the var-cov matrix and \Omega is a rotation which is non-identified by the data, but is identified by your structural model.
Now, let \Sigma(\theta) be the Cholesky decomposition of the var-cov matrix of residuals implied by your estimated DSGE-VAR. Note that \Sigma(\theta) and \Sigma^{*}(\theta) need not be the same! What Del Negro and Schorfheide (2004) do is to set
D(\theta)=\Sigma(\theta) \Omega^{*}(\theta)
i.e., they apply the rotation matrix from the DSGE on the Cholesky decomposition of the reduced form residuals of the VAR. And this is where your identification is coming from,
Finally, keep in mind that It does not mean that the IRFs from the DSGE-VAR are the same to
the DSGE’s IRFs. The resemblance will depend on the wheigh you put in your DSGE (\lambda) .
Hope this helps.
1 Like
Hi Tavinho, many thanks for the reply.
But why Cholesky decomposition and not some other identification scheme? Maybe because Cholesky is convenient not because it is correct?
The term “Cholesky decomposition” is often misinterpreted as a synonym for “short term identification restrictions”. These are two different things. The first is just a matrix decomposition, while the second refers to an identification scheme, which can be achieved by means of a Cholesky decomposition. The first can be used to get the second. For instance, the Cholesky decomposition is also employed when identifying a SVAR with sign restrictions, but what matters for identification is the set of rotations matrices. In a similar fashion, what matters for the identification of your VAR is the rotations matrix.
1 Like
Thanks, Tavinho. I was curious though in using the VAR as ‘evidence’ to validate the DSGE as the VAR cannot replicate the results of a DSGE model (using data simulated from DSGE). And I find the criticism of the VAR in Rudebusch to be kind of valid. Like if I agree with his critiques, then I will put zero weight on the VAR in DSGE-VAR, I guess…
Anyway, my suspicion of using the VAR as evidence to validate DSGE has increased a bit lately…
1 Like