Welfare in TANK model Lee (2025)

Optimal Policy
1

Dear all,

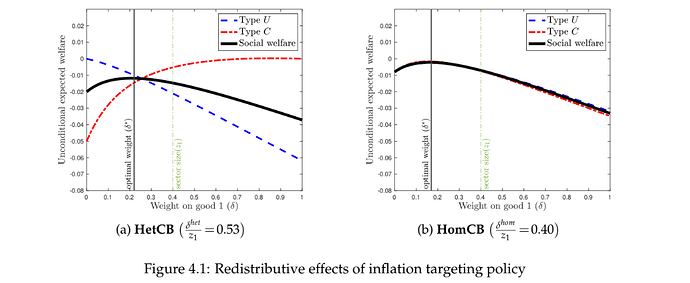
I would like to ask for advice on how to conduct a welfare analysis in Dynare. I am trying to replicate the results from “Optimal Monetary Policy under Heterogeneous Consumption Baskets” by Seunghyeon Lee. I have derived the entire model and implemented the log-linearized (first-order approximation) system of equations in Dynare. However, I am currently unable to reproduce the graph where delta is the parameter on good 1 in the Taylor rule.

image
image1028×423 67.2 KB

image

The author defines welfare as “the expected welfare of each type (measured as deviations from the deterministic steady state).” Could you please advise me on the following:

  1. Which order should the utility function be in the .mod file?
// log utility
U_U = log(cU_level) - nU_level^(1 + varphi)/(1 + varphi);

U_C = log(cC_level) - nC_level^(1 + varphi)/(1 + varphi);

// First order approximation of log utility

U_U = cU - nU_level^(1 + varphi)*nU;

U_C = cC - nC_level^(1 + varphi)*nC;

// Second order approximation of log utility

U_U = cU - nU_level^(1 + varphi)*nU -0.5*cU^2-0.5*varphi*nU_level^(1 + varphi)*nU^2;

U_C = cC - nC_level^(1 + varphi)*nC -0.5*cC^2-0.5*varphi*nC_level^(1 + varphi)*nC^2;

Lowercase letters denote deviations from the steady state.

  1. Which order should I use when running the simulation? Could you please check if this is correct?
stoch_simul(order = 2, periods=1000, irf = 0);
  1. I do not need to implement the the system of equations with the second-order approximation manually in Dynare, right?

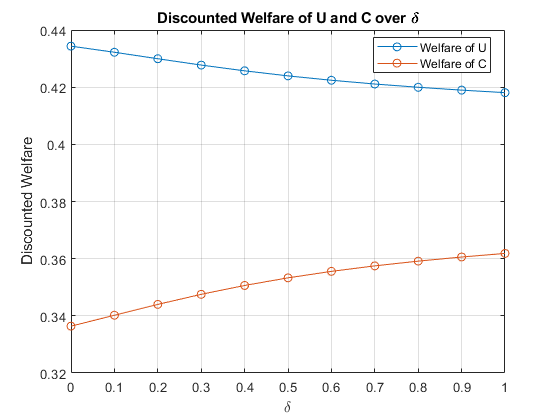
I calculate the sum of discounted utilities in a separate .m file, but the result I get is not correct.
This is my result for the HetCB case.

image
image556×416 8.33 KB

Thank you very much in advance.

2

  1. Generally, you need a second order approximation of the full model. As the paper states

    In the numerical experiment on inflation-targeting policy, we use a second-order perturbation method described in Schmitt-Grohe and Uribe (2004) and measure welfare of each type separately to identify the redistributive consequences of the policy.

    That would mean that working with the log-linearized equations is insufficient.

  2. You should use theoretical moments at second order:

    stoch_simul(order = 2, periods=0, irf = 0);

  3. No, Dynare can do the approximation of the nonlinear objective and equations for you. You can simply enter the nonlinear equations and the recursive nonlinear welfare objective and then do a second-order approximation.

3

Thank you very much for your detailed reply. May I kindly ask for one more clarification? You mentioned that working with log-linearized equations is insufficient, and I completely agree. You also pointed out that I do not need to implement the system of equations with a second-order approximation manually in Dynare. However it would be difficult to use the non-linear system of equatios, as to be consistent with the paper, I would need to express the non-linear variables as deviations from the efficient allocation (in the paper, the author expresses the model variables as deviations from the effective allocation).

  1. Is there any possibility to use the log-linearized system of equations in Dynare to perform a second-order perturbation, as in Schmitt-Grohe and Uribe (2004)? I am almost certain that it is not possible (I already lost the second order terms when linearising the system), but I would like to double-check with you.
  2. If the only way is to return to the nonlinear system of equations, do I need to express the variables as deviations from the effective allocation, or is that not necessary for the welfare analysis?
4
  1. Working with a linear quadratic approach is usually only feasible with involved manual manipulations. See the work of Benigno/Woodford: https://www.nber.org/system/files/chapters/c11445/c11445.pdf
  2. If you go to full second order, there is no point in transforming variables to be in deviations from some efficient allocation. That is typically only necessary for analytical computations or the approach in 1).
1 Like
5

Thank you very much.