Understanding `info` flag output of `stoch_simul()`

Documentation Manual
1

Making a loop through parameters with the stoch_simul() for parameter identification for moment matching. To my best understanding, when the stoch_simul() returns the flag info with value equal to 0, it means that the stochastic simulation ran successfully. But I fail to know which are the other possible values this flag may take, and what they mean. Particularly when not returning 0, I have seen that it may return a 1x2 vector, in some cases with both values being decimal numbers, and in others a whole number accompanied by a zero, like:

info =
  21.000000000000000  29.608813203268074

or

info =
    23     0

I would be grateful if you may help me understanding what this outputs mean, since I think maybe they have information, and so far I’ve failed to find it in the manual. Thanks!

2

I believe only the Dynare team knows the exact meanings of these numbers, but I still would like to partially answer your question upon my own experiments.

First in MATLAB command window, type stoch_simul. MATLAB reports an error: Not enough input arguments. It then gives a routine:

Error in stoch_simul (line 21)
if isequal(options_.order,0)

to stoch_simul.m file. Now open this m-file, and search for the key word info. You will immediately realize that the function stoch_simul calls for a pile of other functions. info is not defined directly in stoch_simul, but in these underlying functions.

Let’s have a try. In my current Dynare version 4.6.4, info can be found in Line 84 of stoch_simul.m:

[oo_.dr, info] = PCL_resol(oo_.steady_state,0);

in Line 89:

[~,info,M_,options_,oo_] = discretionary_policy_1(options_.instruments,M_,options_,oo_);

in Line 96:

[~,info,M_,options_,oo_] = resol(0,M_,options_,oo_);

in Line 105-109:

if info(1)
    options_ = options_old;
    print_info(info, options_.noprint, options_);
    return
end

Then we type these related functions in MATLAB command window as before, finding that only resol will present some useful messages:

>> resol
Not enough input arguments.

Error in resol (line 53)
if isfield(oo,'dr')

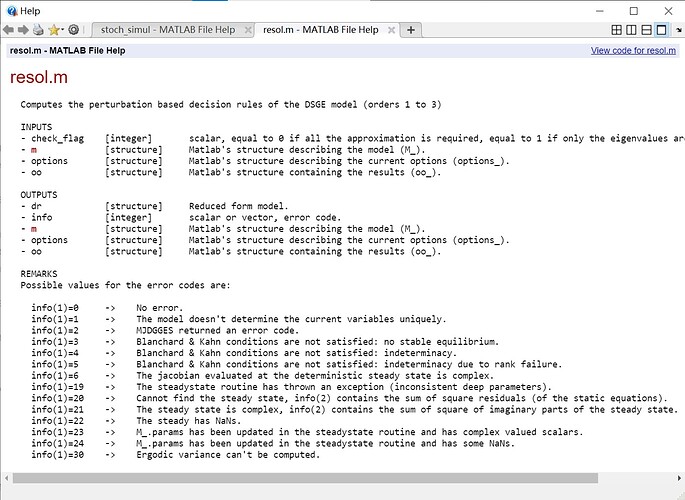
Finally open resol.m. There are lots of info meanings:

% REMARKS
% Possible values for the error codes are:
%
%   info(1)=0     ->    No error.
%   info(1)=1     ->    The model doesn't determine the current variables uniquely.
%   info(1)=2     ->    MJDGGES returned an error code.
%   info(1)=3     ->    Blanchard & Kahn conditions are not satisfied: no stable equilibrium.
%   info(1)=4     ->    Blanchard & Kahn conditions are not satisfied: indeterminacy.
%   info(1)=5     ->    Blanchard & Kahn conditions are not satisfied: indeterminacy due to rank failure.
%   info(1)=6     ->    The jacobian evaluated at the deterministic steady state is complex.
%   info(1)=19    ->    The steadystate routine has thrown an exception (inconsistent deep parameters).
%   info(1)=20    ->    Cannot find the steady state, info(2) contains the sum of square residuals (of the static equations).
%   info(1)=21    ->    The steady state is complex, info(2) contains the sum of square of imaginary parts of the steady state.
%   info(1)=22    ->    The steady has NaNs.
%   info(1)=23    ->    M_.params has been updated in the steadystate routine and has complex valued scalars.
%   info(1)=24    ->    M_.params has been updated in the steadystate routine and has some NaNs.
%   info(1)=30    ->    Ergodic variance can't be computed.

% Copyright (C) 2001-2018 Dynare Team

Alternatively, you may notice the snapshots:

stoch_simul
stoch_simul1392×1012 136 KB

and

resol
resol1395×1018 250 KB

2 Likes
3

You can either look inside get_error_message.m for the meaning or call

get_error_message(info, options_)
2 Likes