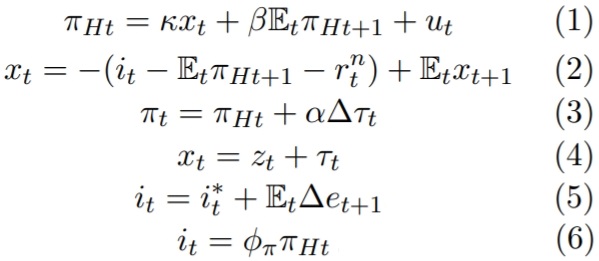Hi all
I am trying to replicate a simplified version of Gali and Monacelli (2005) paper, the equilibrium conditions are provided below. Most variables are standard, but pih denotes domestic inflation, pi denotes CPI, z denotes difference between foreign output, natural level of output and tau denotes terms of trade and e denotes nominal exchange rate.
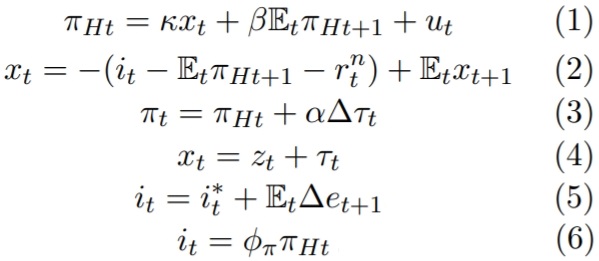
The problem here is the failure of rank conditon (one unit root in the eigenvalues). I think this problem arises because of the ‘Uncovered Interest rate Parity’ equation 5. I searched many GM 2005 codes but it seems that ‘Uncovered Interest rate Parity’ is seldom included in the equilibrium conditions. How can I solve this problem? My mod file is attached below, can someone help me figure it out.
aa.mod (748 Bytes)
Further to my post, cost-push u, natural rate of interest rn, gap between foreign output and domestic
natural level of output z, and the foreign interest rate i* are assumed to be exogenous.
You can see in the above equation system that the exchange rate e only shows up in equation (5). So that equation is supposed to determine it. However, that equation only determines the expected change in the exchange rate, not its level today.
Really thank you for your help, could you give me any suggestions on how to modify equation 5, so that the level of exchange rate can be determined today?
Have a look at DSGE_mod/Gali_Monacelli_2005.mod at master · JohannesPfeifer/DSGE_mod · GitHub
My guess is that your equation (3) can be combined with
s = s(-1) + e - e(-1) + pistar - pih;
where s corresponds to your \tau