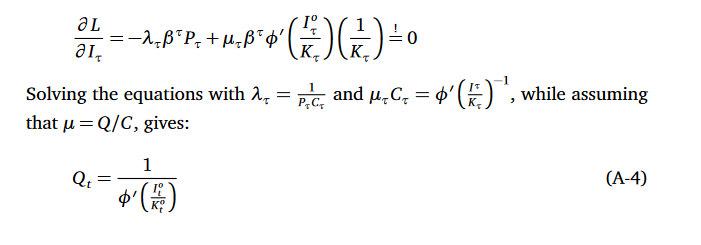I am trying to understand the role of Q_t in this paper (see equations (5) and (6)). According to this other paper (see page 11) Tobin’s Q seems to be the Lagrange parameter for the capital accumulation constraint (i.e. the shadow price of capital). However, in Gali et al. I can only derive equations (5) and (6) by assuming, that Q is the Lagrange parameter times the consumption. I dont understand where this discrepancy comes from.
Thanks!
Please expand on your computations. But often people use Q_t\Lambda_t as the Lagrange multiplier on the law of motion for capital.
Equation (A-4) on this picture is equation (6) in Gali’s paper. I simply don’t know if I made a mistake or if mu=Q/C is s.th. that I don’t yet understand.
I have to admit that I also lack the intuition for what ‘shadow price of capital’ is supposed to mean.
Start with the following Lagrangian where \Lambda_t is the Lagrange multiplier for real payoffs (thus the division by the price level on the nominal budget constraint) and Q_t\Lambda_t the multiplier on the (real) law of motion for capital (the multiplication with marginal utility \Lambda_t helps to turn Q_t from units of resources to utility):
\max L = {E_0}\sum\limits_{t = 0}^\infty {{\beta ^t}\left( {\ln {C_t} - \frac{{{\Lambda _t}}}{{{P_t}}}\left[ {{P_t}\left( {{C_t} + I_t^o} \right) + \ldots } \right] - {\Lambda_t Q_t}\left[ {K_{t + 1}^o - \left( {1 - \delta } \right)K_t^o - \phi \left( {\frac{{I_t^o}}{{K_t^o}}} \right)K_t^o} \right]} \right)}
You will immediately get
\begin{gathered}
\frac{{\partial L}}{{\partial {I_t}}} = - {\Lambda _t} + {\Lambda _t}{Q_t}\phi '\left( {\frac{{I_t^o}}{{K_t^o}}} \right) = 0 \Rightarrow {Q_t} = \frac{1}{{\phi '\left( {\frac{{I_t^o}}{{K_t^o}}} \right)}}
\end{gathered}
You can also check that the 1/C in your approach comes from marginal utility \Lambda_t=1/C_t