The results of occbin

Occbin
1

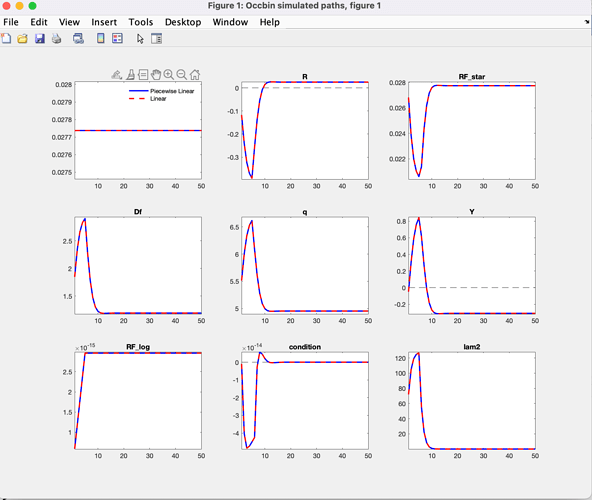
Hi professor, I was running a model where there is a budget constraints.

The budget constraint is

exp(RF)*exp(Df)/exp(pi(+1))=exp(kappa)*exp(q(+1))*exp(Hcf);

RF is mortgage rate, Df is debt at time t, kappa is the LTV, q is the housing price, Hcf is housing volume. lam2 is the Lagrange multiplier of budget constraint. ‘condition’ is the auxiliary variable to check the whether the budget constraint is binding.

condition=exp(RF)*exp(Df)/exp(pi(+1))-exp(kappa)*exp(q(+1))*exp(Hcf);

Then I put

[name='debt', bind='mortgage']
lam2=0;
[name='debt', relax='mortgage']
exp(RF)*exp(Df)/exp(pi(+1))=exp(kappa)*exp(q(+1))*exp(Hcf);
1/exp(Ccf)=beta_tilda*exp(RF)/exp(pi(+1))*(1/exp(Ccf(+1))+lam2(+1));

condition=exp(RF)*exp(Df)/exp(pi(+1))-exp(kappa)*exp(q(+1))*exp(Hcf);

However, the results confused me a lot. It seems that the linear and piecewise linear model have nothing different to show. In addition, when condition is below zero, the lam2 doesn’t equal zero, which isn’t consistent with what I put in occbin constraint. Could you please give a hint about why this happen?Thank you so much for your help.

2022-09-25 21.53.25
2022-09-25 21.53.251826×1540 227 KB

I am uploading whole files for your reference. Thank you again for your help.
test.zip (5.5 KB)

2

Your implementation is

occbin_constraints;
name 'mortgage'; bind lam2<=0; relax condition>0; 
end;

So the constraint will be binding if lam2 drops below 0. But that is not the case in your simulations. The relax-condition is only evaluated if you are in the binding regime. Also note that 1e-14 is 0 for all practical purposes.

3

Thank you professor for your help. I have another follow-up question. It seems that the convergence of occbin is shock surprise sensitive. Sometimes, when I change the values of shock surprise, the otherwise not convergent occbin becomes successfully convergent. Is that normal? Does that mean that something might go wrong with my model? How do I understand this phenomenon?

4

Without knowing more details, it is impossible to tell.