Hi all.
I am trying to model fiscal policy in the pandemic. The pandemic is model as “the probability of outbreak of pandemic” (variable prob in my mod file). There are two industries in my model, one produces general goods, another one produces healthcare. Health goes directly into utility and the evolution of health looks like capital. The modeling of fiscal authority is conventional.
But I have a problem related to forward-looking variables and eigenvalues (posted below):
“There are 13 eigenvalue(s) larger than 1 in modulus for 13 forward-looking variable(s). The rank condition ISN’T verified! … Blanchard & Kahn conditions are not satisfied: indeterminacy due to rank failure.”
Number of eigenvalues exactly match the number of forward-looking variables, but the problem still occurs. I don’t know how to fix the problem, my mod file is attached. Can someone help me.
ben.mod (6.9 KB)
Both the steady state and the timing do not make sense. For example, the steady state for
kg=2.41589e-13, which is essentially 0. Moreover,
%(27) government capital evolution
kg(+1)=ginv+(1-deltak)*kg;
%(28) health evolution
h(+1)=(ch+(1-deltah)*h)*(1-prob*tri);
should usually hold not just in expectations.
Thank you professor. I improved the model according to your suggestion, it works. So thank you again.
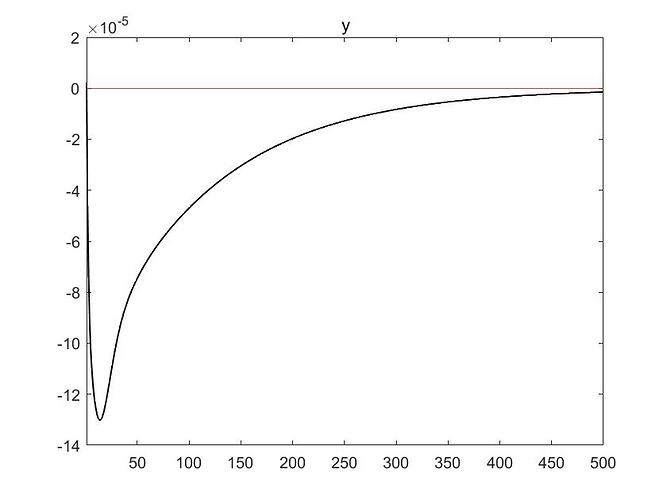
But I still have a question, I give a 1% shock in the probability of outbreak of pandemic and the irf looks like this. It takes about 500 periods for the economy to recover (in terms of output). Pandemic probability shock is only shock that is so different, all other shocks are normal. This result is unexpected. Because I’ve never had any experience modeling epidemics, I don’t know if this result is correct, the effect of covid19 is so long-lasting for economy. What is your opinion?
You need to find out why that is the case. Is it the exogenous process that is so persistent or the endogenous dynamics? Note that many models feature a lot of persistence. Here, the half-life of the shock is about 50 periods.