The problem of IRF

Stochastic simulations
1

Hi everyone, I have a question of coding.
Here is my code:
c1002.mod (8.7 KB)
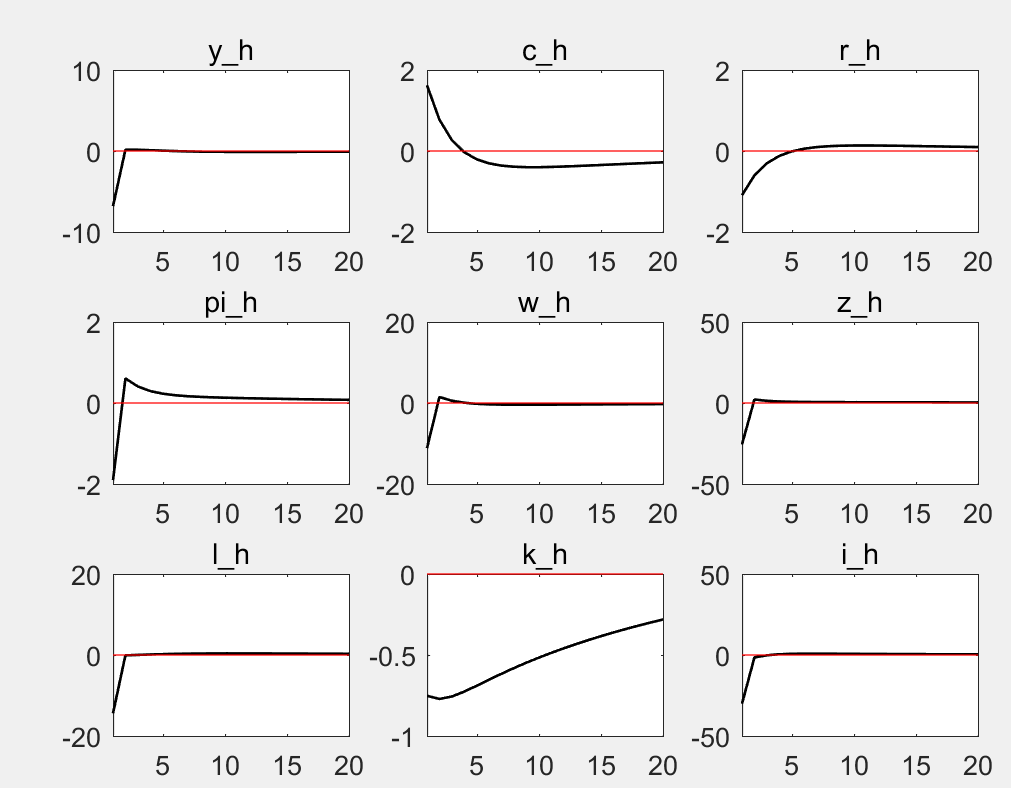
I don’t find any wrong in calculation by myself, but I found that when I add a shock to the foreign interest rate, the IRF looks like this:

image
image1011×788 15.7 KB

As you can see, I only impose a shock of 0.01, but the response of some variables reaches 5.
Does this mean there is a problem with the code?
Thanks for any help!

2

Yes, that is strange, because everything is in percentage deviations in your model. But your model also seems to have a strange unit root. You can see that if you set the IRF horizon to e.g. 2000 periods.

3

Thanks for your reply, professor jpfeifer!
Could you please offer me some idea of how to debug?
Thank you!

4

Only the generic one: check all your equations.

5

Thank you very much!
And I have a question about steady state:
I get the steady state of housing price from the house producer (likes capital producer), and in the model block, I get the housing price from the FOC of family.
Is it reansonable, or the formular in the steady state block and in the model block should come from the same department?
Thanks for your help.

6

I don’t really understand the question. You are dealing with a simultaneous equations system. Everything is jointly determined in the end.

7

Thank you for your reply!
I think maybe there are something wrong with my log-linearization.
Could you please offer me the following equation’s log-linearization version?
k^(-sigma_k) = c(-1)^(-sigma_c)*q(-1) - (1-delta)*c^(-sigma_c)*q
I experimented with several of the log-linearization that I had learned, but I’m not sure my calculations are right and I have no idea of how to verify it.
Thanks for your help.

8

It should be

\begin{gathered} k_t^{ - {\sigma _k}} = c_{t - 1}^{ - {\sigma _k}}{q_{t - 1}} - \left( {1 - \delta } \right)c_t^{ - {\sigma _k}}{q_t} \\ - {\sigma _k}{k^{ - {\sigma _k} - 1}}\left( {{k_t} - k} \right) = - {\sigma _k}{c^{ - {\sigma _c} - 1}}q\left( {{c_{t - 1}} - c} \right) + 1{c^{ - {\sigma _k}}}\left( {{q_{t - 1}} - q} \right) - \left( {1 - \delta } \right){c^{ - {\sigma _c} - 1}}q\left( {{c_t} - c} \right) + \left( {1 - \delta } \right)1{c^{ - {\sigma _c}}}\left( {{q_t} - q} \right) \hfill \\ - {\sigma _k}{k^{ - {\sigma _k}}}\frac{{\left( {{k_t} - k} \right)}}{k} = - {\sigma _k}{c^{ - {\sigma _c}}}q\frac{{\left( {{c_{t - 1}} - c} \right)}}{c} + q{c^{ - {\sigma _k}}}\frac{{\left( {{q_{t - 1}} - q} \right)}}{q} - \left( {1 - \delta } \right){c^{ - {\sigma _c}}}q\frac{{\left( {{c_t} - c} \right)}}{c} + \left( {1 - \delta } \right)q{c^{ - {\sigma _c}}}\frac{{\left( {{q_t} - q} \right)}}{q} \hfill \\ - {\sigma _k}{k^{ - {\sigma _k}}}{{\hat k}_t} = {c^{ - {\sigma _c}}}q\left( { - {\sigma _k}{{\hat c}_{t - 1}} + {{\hat q}_{t - 1}}} \right) - \left( {1 - \delta } \right){c^{ - {\sigma _c}}}q\left( {{{\hat c}_t} + {{\hat q}_t}} \right) \\ \end{gathered}
9

Thanks for your reply!
If there are only three variables have strange IRF like the picture above, dose it stills means that the problem of unit roots still exists, or it can be ignored?
Thanks for your reply!

10

I don’t think there is a general answer. You are the model builder and should know whether there should be a unit root.

11

Dose it means that if I can make sure that the problem of unit root is no exist, although some IRF pictures seems strange , they can be used to analyse (if I can) as well ?
And whether the respone of some variables reaches 2 is reansonable in some cases (with a shock if .01) ?
Thanks for your reading.

12

It is impossible to answer these questions without having built the model.