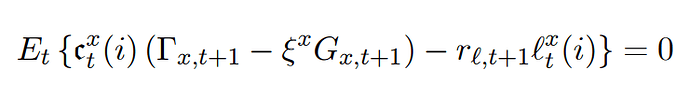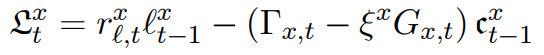Dear Prof. Pfeifer,
I have read Kumhof and Barrdear’s paper “The Macroeconomics of Central-Bank Issued Digital Currencies” multiple times, including the supplementary paper, but cannot understand why bank loss is not strictly 0 at all time. In the main paper attached, because of main equation 27, it seems to me that loan loss equation of 35 should equal zero at all periods. Although they say equation 27 only holds in ‘expectations’ and therefore loan loss is not zero att all time, I dont not undersand it mathematically. I think if you put both equations in dynare, loan loss will become zero at all periods because the expectation thing doesnt change the math, as I understand (which I am surely wrong but dont know why). I have also attached the supplementary paper in which the contradiction I have occures again in pages 9 and 10. As you can see in the supp paper, at pages 9 and 10, both banks’ zero profit based equations (equations of 1.4.2) and loan loss’ equations (equations of 1.5.1) are core functions and used in their simulation. The supplementary paper is freely available at https://www.sciencedirect.com/science/article/abs/pii/S016518892100083X
Thank you in advance.
kumhof_main.pdf (902.8 KB)
kumhoff_supp.pdf (382.2 KB)
Imaging doing a fair coin flip where you win 1 dollar for heads and lose 1 dollar for tails. Your expected profit ex ante will be 0. But after flipping the coin, you will either have won or lost a dollar.
Thank you very much for your response. But what I don’t understand is how does this show itself in a dynare piece of code? If I implement this part in a typical medium scale DSGE model and just type in the equations, obviously the bank loss will become zero. So how does the “this only holds in expectations” part and your explanation show itself in the code? If we just type in the bank zero profit equation and the bank loss equation, as they are in the paper which are included below, directly in our medium scale DSGE dynare code it will obviously result in zero bank loss (am I wrong?). How should it be coded so it wont become zero at all periods based on your explanation?
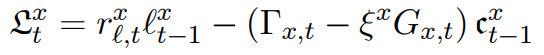
The key is in the timing. Dynare’s timing convention is that each equation in stochastic models is enclosed by conditional expectations. If a condition is dated t+1, it only holds in expectations.
Oh, thank you. Previously I thought shifting the time periods of the final equations’ dynare code won’t change the dynamic of the IRFs. I didnt know that makes a differnce.