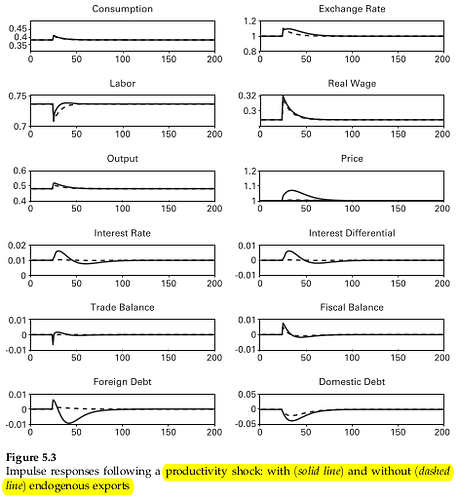
In a multi-sector DSGE model with a tradable sector, export is sometimes modeled as follows:
Let Y^{T}_t = A^{T}_t f(K^{T}_t, L^{T}_t) be the production of tradable goods. And assume that Y^{T}_t is either consumed domestically (C^{T}_t) or exported (X_t). Thus, Y^{T}_t = C^{T}_t + X_t.
In some models, X_t is stochastic, so a productivity shock does not affect export (X_t). If I want stochastic changes in productivity (A^{T}_t) to affect X_t (i.e., supply-driven changes in export), can I define an export function as follows?X_t = X^s_t(\cdot) + g(Y^T_t). Not necessarily an additive function but an export function with both exogenous and endogenous parts.
Where X^s_t(\cdot) is the stochastic part of changes in export (e.g., due to stochastic changes in export demand), and g(Y^T_t) is the endogenous part of export where g is a function of tradable production (Y^T_t).
I did something like this, and the model is fine. But not sure if that is right. I want to capture something like the effect of tradable productivity shock on export.
You are the model builder, so you are allowed to do this. The question is whether referees will buy it.
What is the economic mechanism you had in mind? A more common mechanism is to have a downward-sloping demand curve for exports where total exports depend on the endogenous relative price of exports and exogenous foreign output.
X_t=\left(\frac{P_t}{P^*_t}\right)^{-\varepsilon}Y^*_t
A TFP shock will then decrease the price of exports and increase demand.
Many thanks for the reply prof. Pfeifer. My model is for a low-developed country. Y^T_t is agricultural goods, and X_t is cocoa beans (i.e., the part of agricultural goods exported). The domestic cocoa producer price, however, is fixed by the government, unlike the other non-exported agricultural goods.
To reflect that in the model economy, I kinda fixed the domestic cocoa producer price (in my cocoa export demand function) to a constant, which gave the problem of TFP shock not being able to affect X_t. Something like: X_t = (\frac{\bar{P}}{P^*_t})^{-\epsilon} Y^*_t
As a result, I wanted to explore the effect of TFP on X_t via other endogenous variables like X_t = (\frac{\bar{P}}{P^*_t})^{-\epsilon} (Y^*_t) (Y^T_t)^\eta or X_t = (\frac{\bar{P}}{P^*_t})^{-\epsilon} (Y^*_t) (rer_t)^\eta, where rer_t is the real exchange rate. But like you said, it is kinda unusual and maybe referees will not buy it.
Maybe I need to forgo the fixed domestic cocoa producer price assumption. But actually, it is fixed by the government in reality.
May I also kindly ask a related question. TFP shock does not always decrease the domestic price of export, right? I have seen a positive price-output relationship in some books after a TFP shock as in the example below. Y_t = A_t \text{CES}(K_t, L_t), Y_t = C_t + G_t + X_t, and export = X_t = f(rer_t). They explain that the exchange depreciation increases export demand, and price increases as a result of this higher demand.
Thanks for the reply prof. Pfeifer. Sorry for the confusion. May I clarify a little about my problem. Sorry for long responds.
I want to capture
- The effect of an agricultural productivity shock on cocoa output and,
- The effect of cocoa price shock on cocoa output
So my analysis is really about cocoa output (which is part of Ghana’s agricultural output) and not cocoa export per se. I had assumed that cocoa output \approx cocoa export for the following reasons:
- Only a small percentage of cocoa output (3.4%) is consumed locally. The rest is exported.
- Correlation between cocoa output and cocoa export is about 0.5
This kinda influenced me to consider cocoa export and cocoa output as the same variable (X_t) in my DSGE model. But it seems that would be incorrect.
Instead, can I consider the following (to separate cocoa output and cocoa export)?:
-
Y_t = f(K_t, L_t) is agricultural output
-
Y_t = Y^{nc}_t + Y^{c}_t, where Y^{c}_t is cocoa output (not cocoa export (X_t)). Y^{nc}_t is non cocoa agricultural output. World cocoa price P^c_t is stochastic. Price of non-cocoa agricultural goods (P_t) is endogenous. And I can define an incomplete exchange rate pass through relationship linking P^c_t and P_t. Not sure if this is possible though.
- Then I define cocoa output Y^{c}_t = f (\frac{{P_t}}{P^c_t}, X_t). Empirically, studies have found that an increase in \frac{{P_t}}{P^c_t} causes Ghana’s cocoa output to fall because people smuggle it to other neighboring countries after a shock to world cocoa price. This is the main thing I want to capture.
- And then I can define cocoa export demand the usual way. X_t = (\frac{{P_t}}{P^*_t})^{-\epsilon} Y^*_t. So I have ignored the fixed exogenous domestic cocoa producer price assumption. And also now TFP affects both cocoa output (Y^c_t) and cocoa export (X_t) through P_t.
If it does not make sense, then I will just consider Y_t simply as cocoa output and not agricultural output.
I am still puzzled by what you are writing.
suggests that there is a problem with measured output, not actual output. Then this is something you need to measure.
How would you explain that the correlation between cocoa output and cocoa export is about 0.5? Initially you told a story about TFP, i.e. a domestic shock. Now you seem to be saying that the world market price changes, i.e. it’s a foreign shock.
1 Like