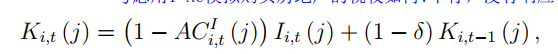The confusion of log-linearize

General DSGE Modeling
1

Hi everyone, I am a student in DSGE.
I feel confuse about the linear version of a fomular.

Here is the orginal formular: (1-AC=1 in the dynare code)
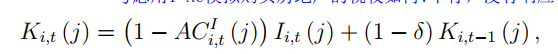
image

I found that the dynare code writted by the author is:

i_h = k_h-(1-delta_h)*k_h(-1);

but the code is model(linear).

I think the correct version of log-linearize is:

i_h * Ihss = k_h*Khss-(1-delta_h)*k_h(-1)*Khss;

Because the setting of the steady state is not equal to 1, so I think the ‘ss’ should be added to the log-linearized version.

Here is the orginal code:
nk2c0100.mod (6.8 KB)
The code I am talking about is in line 99, ‘aa’ and ‘fs’ is parameter which can be ignored.

Here is the code changed by me, I add ‘ss’ into the code:
nk2c0101.mod (7.1 KB)
The code I am taliking about is in line 106, after doing so ,I found the IRF is changed. The effect of the shock was reduced.

Could anyone tell me which log-linearized version is correct?
Thank you very much!

2

You are right that with additive equations, the steady state values should generally show up. Thus, the first version is usually incorrect.

3

Thanks for your reply, professor jpfeifer!

I also found that the log-linearized version of the orginal version also used in the following paper, as is showed in the following picture:

cbd6634410c8274c8c241d12a9136b7
cbd6634410c8274c8c241d12a9136b7712×502 39.7 KB

Here is the paper:
christensen2008BGG.pdf (1.9 MB)

//So, I think the orginal log-linearized version made some sense, maybe? Because other authors can use this way to write papers.

//And I found that use different ways of log-linearized will provide different IRF, as is showed of the result of the .mod file above. If both ways are reasonable, which result should I believe?

Once again, thanks for your help. Merry Christmas!

4

Have a look at your linearization:

i_h * Ihss = k_h*Khss-(1-delta_h)*k_h(-1)*Khss;

Divide both sides by Khss:

i_h * Ihss/Khss = k_h-(1-delta_h)*k_h(-1);

and realize that \delta=\frac{I}{K} such that

i_h * delta = k_h-(1-delta_h)*k_h(-1);

which is identical to Christensen/Dib, but inconsistent with a linearization without a prefactor.

5

Thanks for your reply, best wishes to you!

And I have the other question:
If I change the fomular:

i_h  = k_h-(1-delta)*k_h(-1);

into

 i_h*(1-tax)  = k_h-(1-delta)*k_h(-1);

(tax is a parameter)

Dose the log-linearize version of

i_h*(1-tax)  = k_h-(1-delta)*k_h(-1);

still

i_h * (1-tax) * delta = k_h-(1-delta)*k_h(-1);

？
In others words , does the fomula σ=I/K still apply after I changed the fomula?

Thank you very much!

6

No. i_h*(1-tax) = k_h-(1-delta)*k_h(-1) implies \frac{I}{K}=\frac{\delta}{1-\tau}