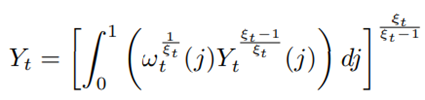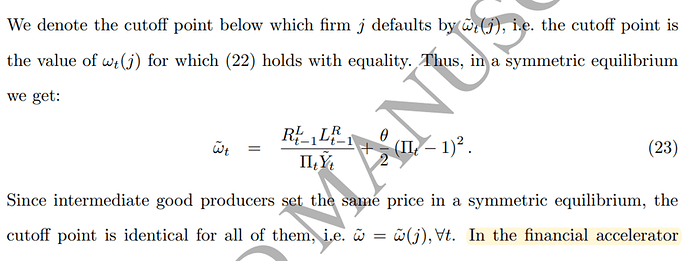The concept of symmetric equilibrium

General DSGE Modeling
1

Hello every one
I have a question about the concept of symmetric equilibrium

Thank you for your guidance

I have seen in the articles : we assume a symmetric equilibrium in the intermediate goods sector, i.e. firms are identical regarding their optimal factor demands as well as pricing decisions
In terms of formulation, they also remove the J index:
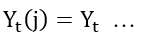
image

Now my question is, what is basically the concept of symmetric equilibrium?
In terms of formulation, I understand the removal of j index, but I don’t understand conceptually.

How is it possible that the production of individual producer (Y_t (j)) is equal to the aggregate production(Y_t)?

While the technology to produce the aggregate final good is:

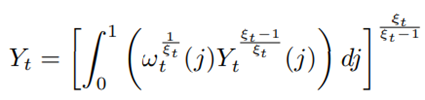
image

2

If you take the last equation
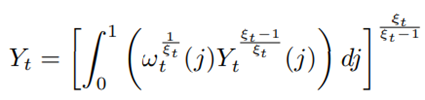
image
and assume that Y_t(j) is the same across all j, you will see that the integral does nothing, but rather whatever Y_t(j) is, Y_t will that value as well. That’s why you can equate Y_t and Y_t(j) in equilibrium.

3

Thank you for your reply.

Is it correct to use symmetric equilibrium in the model that has a idiosyncratic shock?

For example, if our model has a bank sector and a number of borrowers default based on idiosyncratic shock, can we use the assumption of symmetric equilibrium?

in this situation, for example, if the probability of default is 20%, we say that 20% of the firms will default and 80% will not default, in this case, the firms were separated from each other. How can these firms be homogeneous?

For example, it is stated in one of the articles:

image
image975×369 117 KB

My question is, how can we assume that firms are homogeneous, assuming the existence of a idiosyncratic shock that is different for each firm?

I think we can interpret it like this: It is as if there is a representative firm whose default probability is 20% and the probability of not defaulting is 80%. Do you think this is true?

4

The question is whether heterogeneity matters. Idiosyncratic shocks for borrowing costs may not spill over to the pricing decision. Firms may still be symmetric with respect to the pricing. That is what the screenshot above suggests.