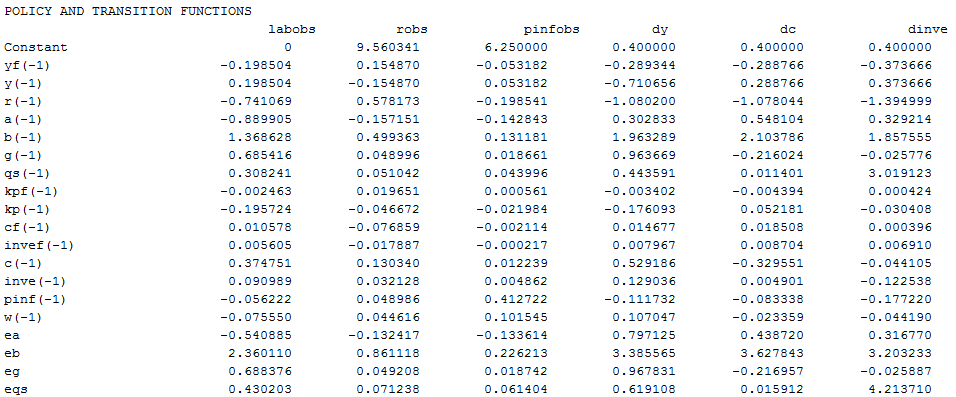
Total Dynare noobie. I’m trying to just solve the state space representation of Smets Wouters 2007. I modified their code with stoch_simuli() to solve a policy function to the second order. For the policy and transition functions I get something like this:
I was under the assumption that the state space form would be s = As(-1)+s(-1)Bs(-1) and y = Cs(-1)+ s(-1)Ds(-1). How am I suppose to convert this to the state space form I have shown?
Hi,
You are missing some terms in the reduced form. It should be something like:
y_t = y^{\star}+\Delta +A \tilde y_{t-1} + B \varepsilon_t + C \left(\tilde y_{t-1}\otimes \tilde y_{t-1}\right) + D \left(\tilde y_{t-1} \otimes \varepsilon_{t-1}\right)
+ E \left(\varepsilon_{t-1}\otimes \varepsilon_{t-1}\right)
where \tilde y_t = y_t-y^{\star} is the deviation to the steady state. The vector \Delta, and matrices A, B, C, D and E are available in oo_.dr, you don’t have to build them from the table of policy and transition equations. See the reference manual here.
Best,
Stéphane.
Hi Stephane,
I’m using what is probably an old Dynare and when I compute up to the third order in the dr structure I have ys, ghx,ghu,gx,Gy ans matrices (and others). Is there a way to convert that to G0,G1… as well as the measurement equation coefficients. Thanks,
Cameron
Edit: I upgraded to 4.5 but when I run it for order 3 I only get order_var, inv_order_var, kstate, transition…,ys,g_1, ghx, ghu, variables in the dr folder and I’m not sure how to construct all the reduced form equations from them.
Actually I don’t know if I’m doing the right thing. I want to get the state space as a function of coefficients and do estimation outside of Dynare. This seems to just solve the model for a fixed point. Is there a way to do that?
Cameron
Hi Cameron,
I probably do not understand what you are trying to do… If you want to estimate the model (using a higher order approximation) you need to have a reduced form routine that given the values of the parameters, of the shocks and the states, returns the next period state variables. It is not possible to have this reduced form as a function of the parameters, but only as a function of the parameters values, because we do not have closed form expression for the reduced form model.
So if you want to estimate a model, for each vector of parameter you need to compute the steady state, evaluate the Jacobian and Hessian matrices at the steady state, compute numerically the reduced form (i.e. ghx, gnu, ghxx, …). And then you can iterate on equation I wrote in my first response.
Dynare provides nonlinear filters (particle filters) based on a second order approximation of the model. You can look at the routine:
matlab/reduced_form_models/local_state_space_iteration_2/local_state_space_iteration_2.m
to see how we use the matrices in oo_.dr to do that. I plan to implement the same routine for third order approximation in Dynare 4.6.
Best,
Stéphane.
@cameronfen Let’s step back for a moment. The Smets/Wouters 2007 code implements an already linearized model. How do you then solve it at second order? All higher order terms are 0 in this case. The decision rules you pasted above do not contain any higher order terms.
I guess I’m not being clear, a large part due to not understanding whats going on. I’m looking at Wouter de Haan’s slides: http://www.wouterdenhaan.com/numerical/slidesbayesian.pdf on slide 39 it mentions, a_{k,k}, a_{k,z} all these are functions of deep/structural parameters \Psi. Also in Solution and Estimation of DSGE models (version: http://www.hoover.org/sites/default/files/fernandez-rubio-shorfheide-hbofmacro_solveestimate_v1.pdf), on printed page number 70 and 76 in acrobat, it lists the matrices as a function of the deep parameters. I want dynare to output those matrices as shown on page 70 as a function of those (deep/structural) parameters, but preferably up to second or third order. As you probably assumed my familiarity in this area and intelligence is higher than it actually is, please keep it dumb. If I’m still asking the same thing and you would just be repeating yourself please feel free to ignore.
DSGE models are usually very nonlinear. We approximate the true nonlinear solution by Taylor approximation of a particular order. You now want a second order polynomial. But the model you are referring to, the Smets/Wouters 2007 model, was linearized, i.e. a first order Taylor approximation was performed. If you now go to second order, all second order terms will be 0 because the model was already linearized. Have a look at your mod-file. Are the FOCs linear or nonlinear?
Looked at the Smets Wouters model, damn it you’re right, all the equations are linear. That was really a stupid of me. Anyway I appreciate the help! Now presumably they had nonlinear structural equations that defined their DSGE and then they took a first order approximation of those equations. I assume Dynare can from the structural equations find out the Taylor series of the policy function to some order like 2 or 3? I’m not really interested in solving the second order equations and not particularly knowledgable there. Is there a way I can get my hands on some well known, the more complex/large state space the better (although I’ll have to enter the equations by hand I think so that has to be a constraint on the state space size), nonlinear (more orders better but again hand entering) DSGE model which has defined A, B, C, D, E etc. (in stephan-a original comment) in terms of the structural parameters to perform estimation on? Or take a set of the nonlinear structural equations and have Dynare spit back the 2 or 3rd order taylor approximation (as a function of deep parameters) of the policy?