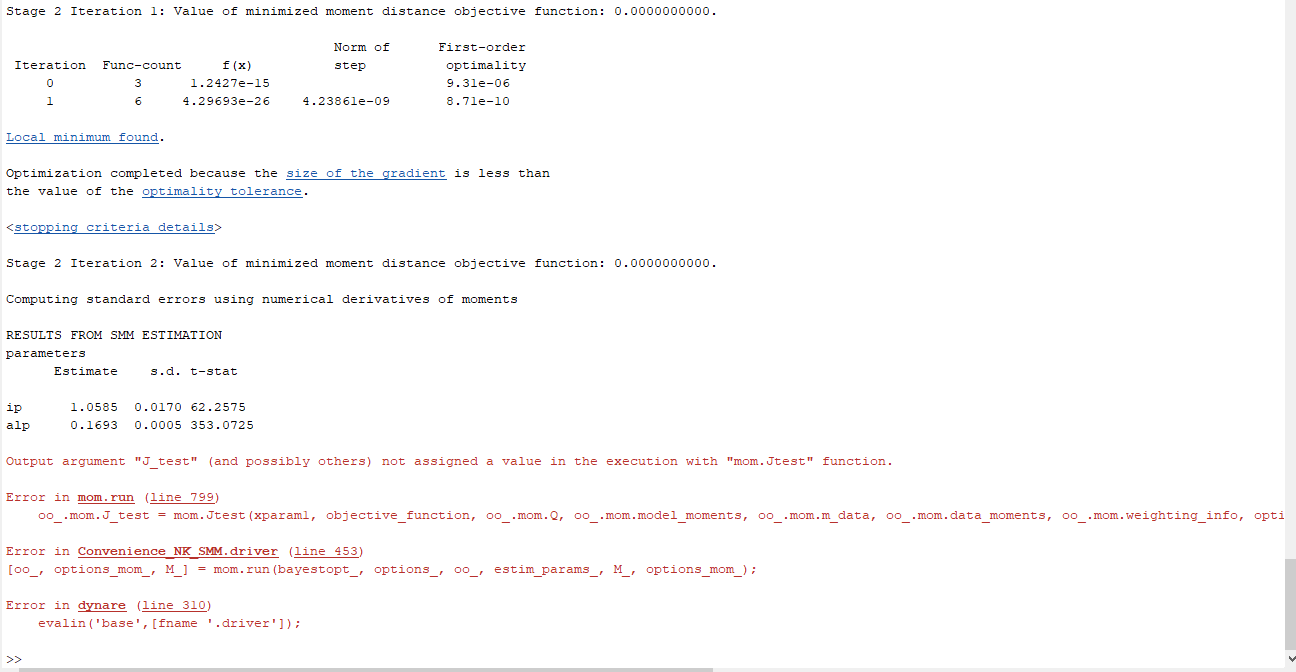
Hi all, I am doing a SMM test now, but my code keeps returning following error:
Thanks for reporting this. It’s a bug with a fix at 🐛 set J_test field to empty in case of just or underidentified case (!2290) · Merge requests · Dynare / dynare · GitLab
Thank you for your response professor, so how do we deal with this problem with this fix?
In addition, could you tell me whether the gradient size small is a big problem for the validity of my estimation?
Hi Professor Pfeifer, is it possible to see a IRF picture after doing SMM with the estimated result in dynare? I have got some weird result so I want to see whether dynare do the job as what I expect.
For example, I am estimating a Taylor rule coefficient with passive monetary policy s the coefficient should be smaller than 1. Denote the coefficient as ip and the deviation of inflation as p. My moment is the deviation of real interest rate RRC, which is 400*(ip-1)*p. Given the mean of my empirical data of RRC is negative, when I give a government spending shock, the inflation p should be positive, and there for, the estimated ip shoud be smaller than 1. However, I keep getting result that ip is slightly bigger than 1. I thought how dynare does the job is to positively shock the model and optimally pick an value for the coefficient we want to estimate, but it seems that it is not the case. Am I correctly interpreting the mechanism? Thank you!
You can run stoch_simul after method_of_moments with the estimated parameters being automatically set.
And sorry, but I do not get the second part.
Thank you professor. The second part is to try to illustrate my confusion. I am estimating the coefficient of Taylor rule (the coefficient on inflation, denote it as α) in a NK model with government spending shock. My moment is the deviation of real interest rate from an exogenous steady state real interest rate. Given the mean of my empirical data is negative (it means that the average real interest rate of my sample data is smaller than the steady state), I expect that the coefficient α is smaller than 1 (passive monetary policy). However, the estimated result is slightly bigger than 1, and the moment actually fit rather well, and the standard error is extremely small (t-test is bigger than 30000, I think it is not good actually). But apparently, with that value of α I can not replicate the empirical result in model. I think I may misunderstand how dynare works actually.
I thought that in doing SMM, dynare will shock the model, (in my model is the government spending shock), and then dynare will automatically find the optimal parameter value. If that is the case, then when dynare shock the model, inflation will increase, and then dynare will assign a small value to α to ensure the decrease of real interest rate. But that is not the case actually. That is why I want to know the mechanism of SMM in dynare.
In addition, could you tell me whether there are any guidance code for MLE or Bayesian guidance code?
By the way, I think that the paper from An and Schorfheide, Bayesian Analysis of DSGE Models, is about using Bayesian estimation?
Hi Professor, but my model include an active fiscal policy that the tax does not response to debt (fix it to zero like Bianchi and Melosi 2017), so it should be fine according to Leeper (1991). Actually, the monetary policy coefficient I got is 1.0002. Once I increase the prior calibrated value to 1.0004 the model will be indeterminate. That is what really confuses me.
Does a calibrated version of the model with a low feedback work? If yes, then it sounds as if your data pushes the model right to the boundary of the determinacy region.
yes, a calibrated version works well (calibrated value is around 0.6)
Then it’s probably about the data.
i am thinking of using bayesian estimation. will it get some different and more plausible result?
There is no way to tell a priori.
