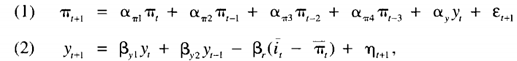Adaptive-expectations
In a paper by (Glenn D. Rudebusch and Lars E. 0. Svensson), they estimate backward-looking autoregressive models (under adaptive expectations) using OLS.
(John P. Judd and Glenn D. Rudebusch) takes the above equations with the estimated parameters and adds (3) an estimated Taylor rule. They do counterfactual analysis using these three equations for different parameters of the Taylor rule.
Rational expectations
Can I do Bayesian estimation in dynare and then use the following equations (with the estimated parameters) to do counterfactual analysis (outside dynare) rather than using an adaptive-expectations model like in the above?
[name='New Keynesian Phillips Curve eq. (22)']
pi=betta*pi(+1)+kappa*y_gap;
[name='Dynamic IS Curve eq. (23)']
y_gap=-1/siggma*(i-pi(+1)-r_nat)+y_gap(+1);
Thus, for example, simulate inflation using the above-estimated equations in dynare and
i=phi_pi*pi+phi_y*y_gap+nu;
where phi_pi<1, assuming, for example, phi_pi<1 in the given period…like in the Burn’s period in the US.
The only difference here is that I wanna use estimated RE equations from dynare and not the adaptive-expectations model as used in the paper by (John P. Judd and Glenn D. Rudebusch) for counterfactual analysis for different taylor rule parameters.
I am not sure I understand the problem. You can pretty much run any counterfactual you like. The only restriction is that the model must satisfy the Blanchard-Kahn conditions.
Thanks for the reply, Prof Pfeifer. I understand your answer. For the counterfactuals I want to simulate, however, BK conditions will not be satisfied since phi_pi<1 in the Taylor rule.
For example,
-
I simulate a model with the policy i=1.212*pi+0.954*y_gap+nu; (no problems here).
-
Then I wanna do a counterfactual simulation with the policy i=0.456*pi+0.230*y_gap+nu;. But BK conditions will not be satisfied.
Of course, one could simulate such a counterfactual scenario under adaptive expectations, and that is what the papers I mentioned earlier did.
My thought
If the parameters in the IS and Phillips curve (under RE) are structural, maybe I can take the following equations below (outside dynare) after estimating the parameters in dynare, and simulate a counterfactual scenario under the policy i=0.456*pi+0.230*y_gap+nu;. So I will have something like (just an example)
pi=betta*pi(+1)+kappa*y_gap;
y_gap=-1/siggma*(i-pi(+1)-r_nat)+y_gap(+1);
i=0.456*pi+0.230*y_gap+nu
And then simulate paths for pi, y_gap and i, but outside dynare. Note that the parameters are however estimated in dynare under RE. The approach sounds feasible? Thanks!
In the papers I posted, they give several reasons for using backward-looking expectations rather than forward-looking expectations model, but it seems one reason they choose to use a backward-looking expectations model is that they can not simulate the Burn’s period for the US (where phi_pi<1 from OLS estimation of the Taylor rule)…although they don’t say.
But yeah, my idea was why not estimate the parameters in the IS curve and Philips curve (under RE and using Bayesian estimation) in dynare. Then take them outside dynare and then do simulations under the policy i=0.456*pi+0.230*y_gap+nu (which will of course violate BK conditions in dynare).
It may be a wrong approach, but I cannot see how for now. Thanks for the reply, and sorry for my long response.