Hi all, I was wondering if anyone could help me with a question related to the Bayesian estimation:
For some object of interest (such as smoothed variables or forecasts), would it be different if we calculate its value in the following two methods?
(1) Calculate its value for each posterior subdraw of the parameters, and then take the average across all subdraws;
(2) Calculate its value by fixing the parameter values to their posterior means.
Intuitively, they should be different, because the object of interest is usually a nonlinear function, say f(\cdot), of the estimated parameters, say \hat{\theta}. So usually E[f(\hat{\theta})] \neq f(E[\hat{\theta}]).
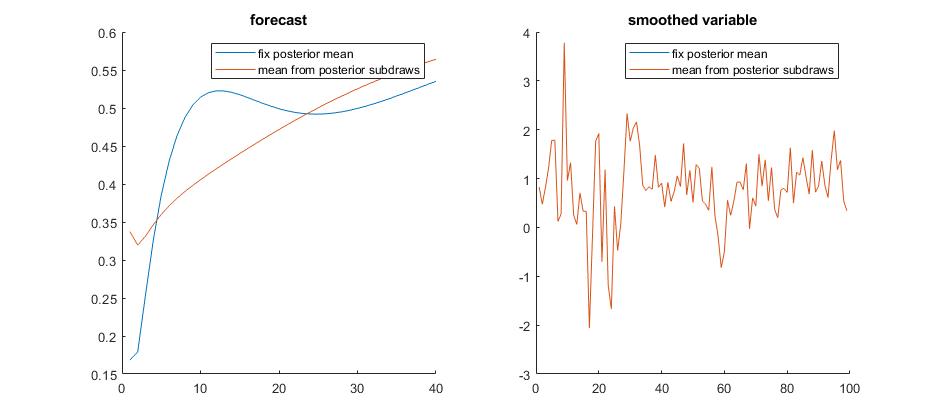
As an experiment, I calculated the values of two objects based on the above two methods in an estimated Smets and Wouters (2007) model. The two objects are the smoothed values and forecasts of the real GDP growth.
Method (1) is how Dynare calculates smoothed variables and forecasts after MCMC draws. So I just took two arrays after a Bayesian estimation:
`oo_.SmoothedVariables.Mean.gdp_obs`
`oo_.MeanForecast.Mean.gdp_obs`
For method (2), I followed the suggestion from this post,
added three lines in “dynare_estimation_1.m”, removed estimation blocks in the mod-file, fixed the parameter values to their posterior means, changed the estimation command to something like
`estimation(smoother, order=1, prefilter=0, datafile=..., xls_sheet=..., xls_range=..., presample=4, mode_compute=0, forecast=40) gdp_obs`
and collected the following two arrays:
`oo_.SmoothedVariables.gdp_obs`
`oo_.forecast.Mean.gdp_obs`
Interestingly, the forecasts are dissimilar but the smoothed variables are almost the same.
How to explain this difference? Did I do something wrong for the second method?