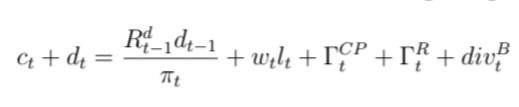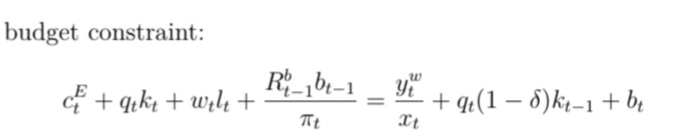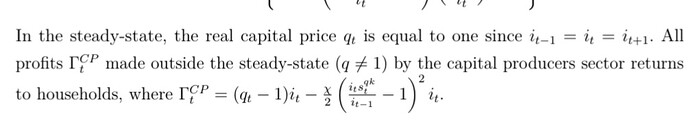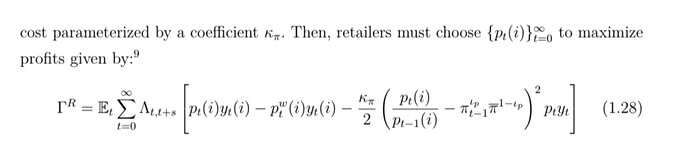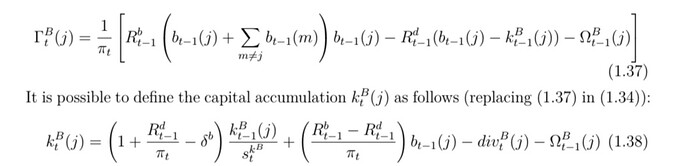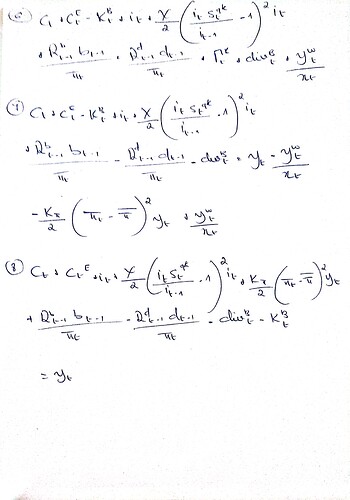Dear all,
I’m trying to derive the resources constraint found in one of the Ph.D. theses I’m currently reading. I’ve contacted the author for clarification but unsurprisingly my message was ignored. The resources constraint is the following:
While the households and entrepreneurs’ budget constraints are:
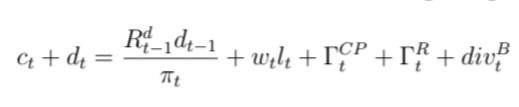
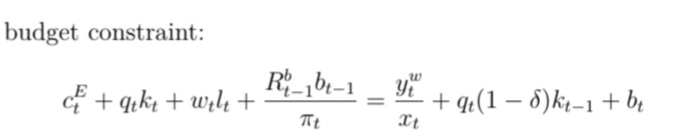
As for the banks, retailers and capital producers profits:
This is my attempt:
I would be eternally grateful for your help and guidance. I’ve spent several days trying to employ all the tricks and substitutions possible but to no avail. The link to the complete Ph.D. thesis can be found here:
https://www.google.com/url?sa=t&source=web&rct=j&url=https://bibliotecadigital.fgv.br/dspace/bitstream/handle/10438/32417/tese_matheus_melo_eesp.pdf%3Fsequence%3D1&ved=2ahUKEwji_rbWv53_AhW3UKQEHYihDKQQFnoECAoQAQ&usg=AOvVaw2g6KXzUknppWBoeB1sfPuO
Looking at the equation, it seems rather standard. What exactly is the problem? Can you try to explain it economically. People will not be able to dig through a thesis.
1 Like
Dear Prof. Pfeifer,
Thank you so much for your response. My confusion comes from the fact that the resource constraint is, to the best of my knowledge, obtained by aggregating the budget constraints of entrepreneurs and households budget constraints but when I try to derive it by hand I end up obtaining a different result which has put into question the correctness of the derivation procedure. As for the goods market clearing condition, it is supposed to abide by the following equation: Y = C + I + G + X - M + ADJ. In this case, the economy is closed and the government is absent modifying the equation into: Y = C + I + ADJ. My question in this case is how are we supposed to interpret dividends? Are they banks’ consumption? Thanks in advance Professor.
My hunch is that this is a typo. Why should dividends appear in the resource constraint if they are just transfers between agents?
1 Like
That’s what I have been wondering. One final question, I’ve summed the budget constraints in the thesis and obtained the following equation:
c_t + c^E_t + i_t + \xi/2 (i_t/i_{t - 1} - 1)^2 i_t + \kappa_{\pi}/2 (\pi_t - \bar{\pi})^2 y_t + \kappa_{k^B}/2 (k^B_t/b_t - \tau)^2 k^B_t = y_t + (1 - \delta^B) k^B_t
Where k^B_t is the bank capital. Does the resource constraint equation I found make sense? Thanks in advance Prof. Pfeifer.
Yes, that mostly makes sense. But why is there no k_{t+1}^B showing up?
1 Like
I believe because bank’s capital is not used for productive purposes and is a regulatory standard for financial intermediaries 
while \delta_B in (1 - \delta^B)k^B_{t - 1} refers to the fraction of resources mobilized to manage it and not the depreciation rate as in the case of entrepreneurs. But I could be wrong 
