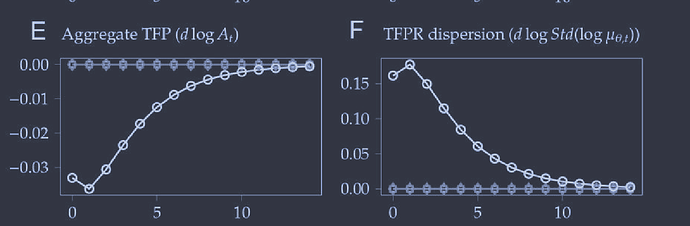
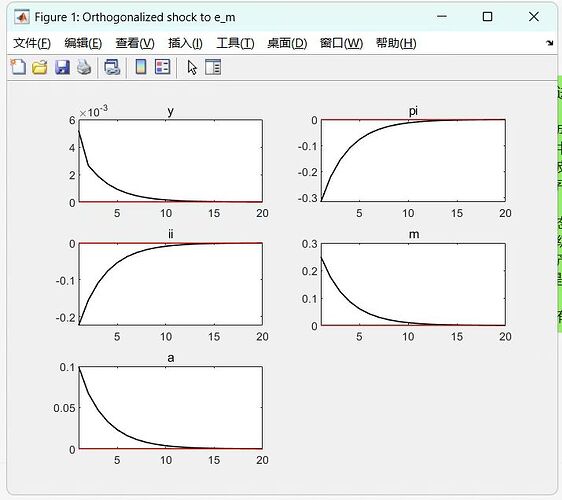
I’m currently working on replicating Proposition 5 using Dynare, which involves dynamic New Keynesian (NK) equations with total factor productivity (TFP) movements. However, I’ve encountered an issue: the impulse response function (IRF) results I obtained differ from those presented in the paper. Specifically, the output response in my results is relatively small, and the direction of the output response and the TFP response are opposite to those in the paper. I would appreciate any insights or suggestions on how to address this discrepancy.
test.mod (1.2 KB)
Check the coefficients.
alpha = (phi/mubar)*(rho*(1+mubar*varphi)-1) ;
kappa_a = 1+beta + phi*(1+(cov/elast)*(1+mubar/varphi));
have mubar*varphi while it is mubar/varphi in the equation you posted.
Thank you for your meticulous review of my code. But in my code, varphi represents the inverse of the Frisch elasticity, which is equal to 1/\zeta. Therefore, you can see that I use varphi to substitute 1/\zeta.
Then I don’t know what is going on. Have you checked the official replication files?
The official replication does not use dynare,so I cannot tell what is different.
But it should be informative about equations, parameter values, etc. The model itself is simply.
Hi professor, thank you for your suggestion. I’ve reviewed the Python code and identified the key issue: the parameters derived from firm-level decisions are endogenous and thus time-varying during the dynamics. This explains why the authors implemented a complex custom solution for solving the dynamic model rather than relying on Dynare.