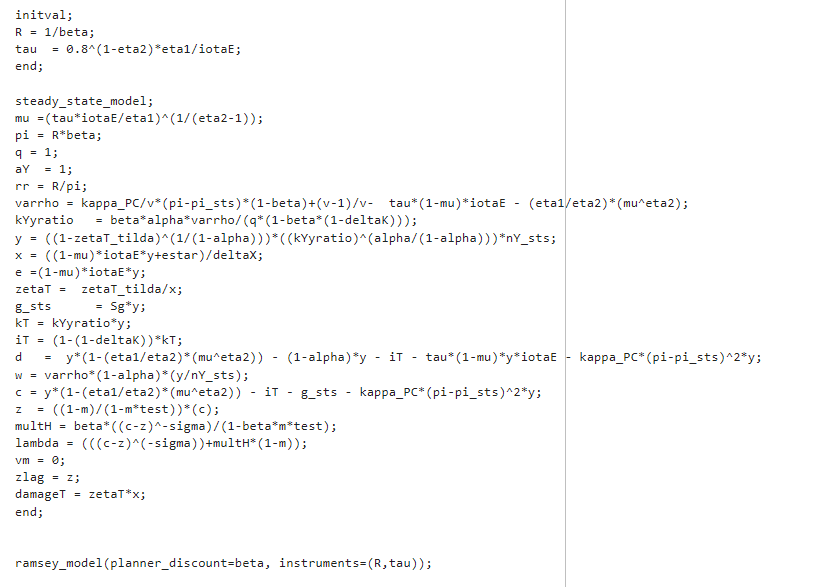
Hi,
I am trying to solve Ramsey optimal policy for two instruments (tax and interest rate). The model is running for usual stochatic simulation with a Taylor Rule and also for each instrument alone.
If I run the mod file for both instruments at once, I get zero residuals for my steady states but I still get the following error:
Error using print_info (line 33)
Ramsey: The solution to the static first order conditions for optimal policy could not be found. Either the model doesn’t have a
steady state, there are an infinity of steady states, or the guess values are too far from the solution
Error in steady (line 143)
print_info(info,options_.noprint, options_);
Could you give me a hint on the error? I computed the steady states conditional on the instruments and set R and tau (instruments) into an initval block. The conditional
steady states are computed within a steady_state_model_block.
I am very thankful for any advise!
Thanks!
I would need to see the full files. But it could be an economic issue in that indeed no steady state for the Ramsey problem exists in this case.
1 Like
I got
Ramseyoptimaltaxmp.mod (4.0 KB)
to run in Dynare 6.1. Basically, the issue seems to be that the steady state for tau is as close to 0 as possible.
1 Like
Thank you, its is running in 6.1 now. So basically, before you have changed the initval for tau it was something like 0.5590 and now the initval is close to zero.
Therefore, I could not find the steady state because the intival was too far away or am I wrong? I just want to understand what was wrong and if the solution makes sense, where tau is close to zero so essential no tax is optimal in this problem.
tau=0 seems to be infeasible for some reason. Dynare had a hard time approaching that asymptote from the starting value you chose.
Thank you very much for your response. I have to think about the model again, it seems strange that the tax is equal to zero.
Thank you for your help!
I am currently working on my other files, where I only have the monetary policy as instrument. I am wondering how I can compute the second or higher order approx. for the ramsey problem? If I change the order in stoch_simul, the irfs do not change. Therefore, I assume that the either the higher order do not matter in this case or I have to code this differently than just changing order = 1 to higher orders.
That is strange. I would need to see the codes.
The IRFs at order=2 are not identical to the ones at order=1 but very close. That suggests that the original nonlinear model is quite close to the nonlinear one.