Dear All:
I am trying to look for ramsey optimal policy in Gali Chapter 8 nonlinear model in Dynare 4.6.4, which this code comes from Prof. Pfeifer. But something is wrong, code is attached below:
I have read most the ramsey policy posts on the dynare forum . I have two question:
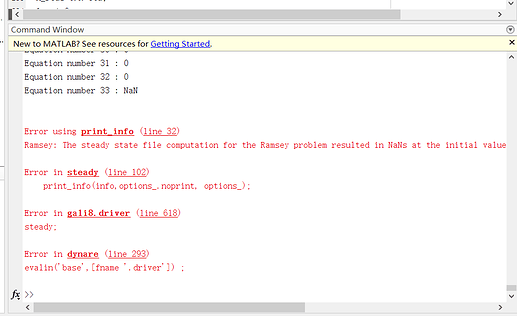
(1) In the state-state-model or _steadystate.m ，Do we not need to set the initial value of the instrument variable？
But, as we can see, If the instrument variable does not have an initial value ，the steady-state value of other variables represented by it may be NAN .
(2) The code run successfully in taylor rule, if we put it in ramsey optimal policy, Do we still need to change the equation in _steadystate.m ?
(3)If we introduce uncertainty shocks into the model, can we still make ramsey optimal monetary policy ?
Thank you so much in advance!
Thanks for your reply, Prof. Pfeifer.
It’s really solve my puzzled.
And I have other two question about ramsey optimal policy:
(1) Is there an example about how to build new _steadystate.m in ramsey policy.
In Talyor rule, I write _steadystate.m follow Willi Mutschler’s video. But his website doesn’t have example about ramsey policy.
(2) As you say, stoch_simul(order=3) may be not the appropriate order. Do you think the correct order should be order=4 or 5, which need to use Dynare++?
Thank you in advance!
Thanks for your reply, Prof. Pfeifer.
I added Ramsey optimal monetary policy to the non-linear model in Gali’s Chapter 8. And I also construct _steadystate.m file.
Everything runs well, but the command window don’t show “Approximated value of planner objective function”.
So I want to trouble you to see where the problem is
(The code runs in Matlab R2020a and Dynare 4.6.4).
You did not call evaluate_planner_objective.
Thanks for your reply, Prof. Pfeifer.
I add evaluate_planner_objective into the code , everything runs well.
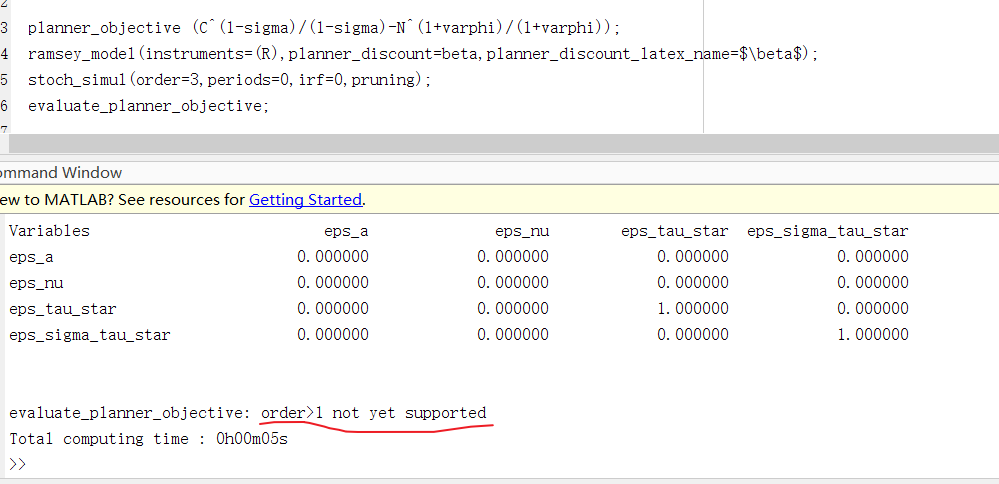
And I introduced ramsey policy into uncertainty shocks, as we all know “stoch_simul” order should be thrid. But command window prompt the following information:
Prof. Pfeifer, so if I would like to ramsey policy in uncertainty shocks, how to I construct the mod file?
I‘m really confused now.
Thank you in advance!
Support for order=3 has only been added in Dynare 4.7. But even then, order=3 only works for conditional welfare. See https://git.dynare.org/Dynare/dynare/-/wikis/NewFeatures
Thanks for your reply, Prof. Pfeifer.
I install Dynare 4.7-beta2.
And I introduce tariff uncertainty shock into small open economy, and I construct IRF in uncertainty shocks model borrowed yours DSGE_mod/Basu_Bundick_2017.mod at master · JohannesPfeifer/DSGE_mod · GitHub.
In taylor rule, the totutility is -19.028, and all the IFRs to the third-order uncertainty shock are in line with expectations, output, consumption and invest decline.
But in the ramsey optimal policy: I have third questions:
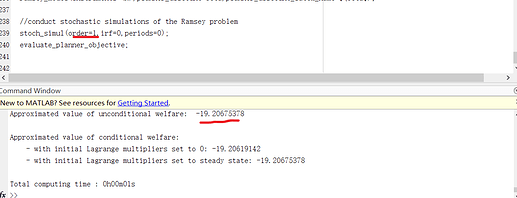
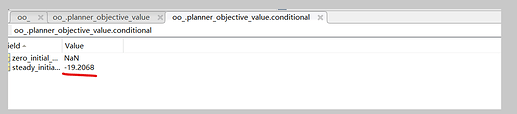
(1) stoch_simul(order=3) and stoch_simul(order=1) ,we can get the same unconditional welfare:-19.2068. I doubt, is this result correct ?
And order 3, the unconditional welfare:
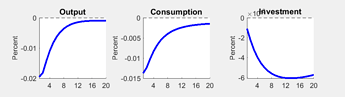
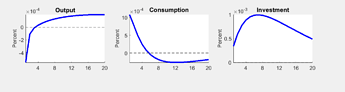
(2) If order set to third in ramsey policy, I can get the IRF in uncertainty shocks as follows: consumption and invest increase, this is against our common sense, so I would like to trouble you to help me see what is wrong ：
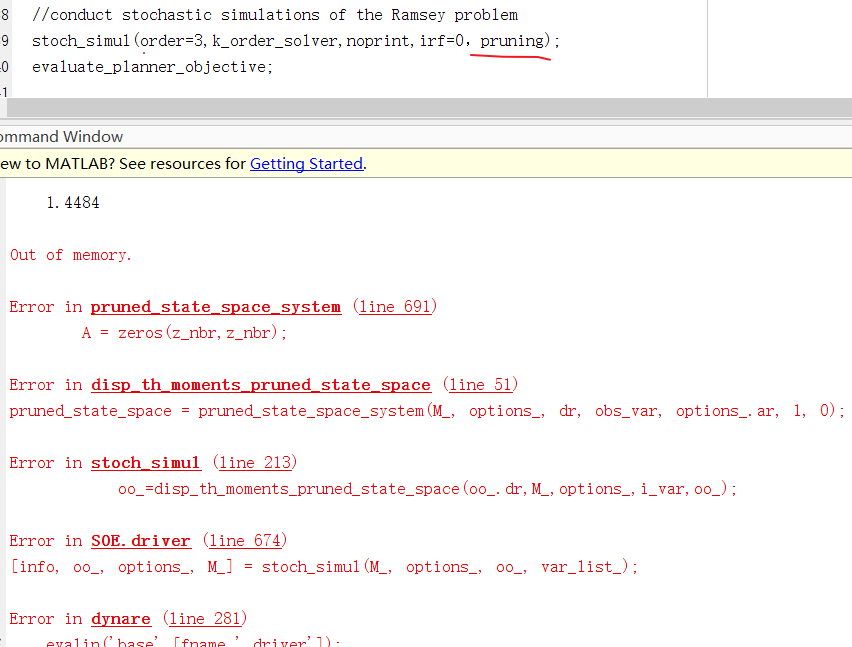
(3) If we add “pruning” into stoch_simul(order=3), the command window report “out of memory” as follows:
Thanks for you help in advance. Prof. Pfeifer.
Can you provide me with the file?
That should be correct. A different way of getting welfare conditional on being in the steady state is:
Y3 = simult_(M_,options_,oo_.dr.ys,oo_.dr,zeros(1,M_.exo_nbr),options_.order);
Welfare=Y3(W_pos,2)
The nonlinear model about small open economy has all been solved with your help, Prof. Pfeifer.
Thank you for your warm and timely answer, which made me fall in love with Dynare.
Thanks!
