Questions on SMM Estimation

[yw3864a]

Hi everyone,

I am currently working on a DSGE model using the Simulated Method of Moments (SMM). I have encountered several issues and have a few questions that I would like to ask for your guidance on. I appreciate any advice or feedback you can provide.

(1) Selection of Estimated Parameters:

How do I generally decide which parameters to include in the estimated_params for estimation? Is it acceptable to select only a subset of parameters for estimation based on my judgment? I am concerned that this might lead to very subjective judgment and may contain bias.

(2)Choice of Matched Moments:

Regarding matched_moments, is the selection of moments also purely subjective? Should I include moments that yield actual data values and theoretical values that are closer, or is there a more objective criterion to follow?

(3) Order of Estimation:

How should I decide whether to use first-order, second-order, or higher-order estimation? My model only works with first-order estimation, but it fails with higher orders. What could be causing this issue? If I am unable to perform second-order or higher-order estimation, is it acceptable to rely solely on first-order estimation results?

(4) NaN in SMM Estimation Results:

In my RESULTS FROM SMM (STAGE 2) ESTIMATION, the standard deviations (s.d.) and t-statistics are showing as NaN. What might be causing this, and how should I troubleshoot and resolve this issue?

(5) Comparison of Data Moments and Model Moments:

When comparing data moments and model moments, do all the moments need to be close, or is it sufficient if most of them are close? What is the acceptable error margin, and what criteria should I use to evaluate the goodness of fit for the model?

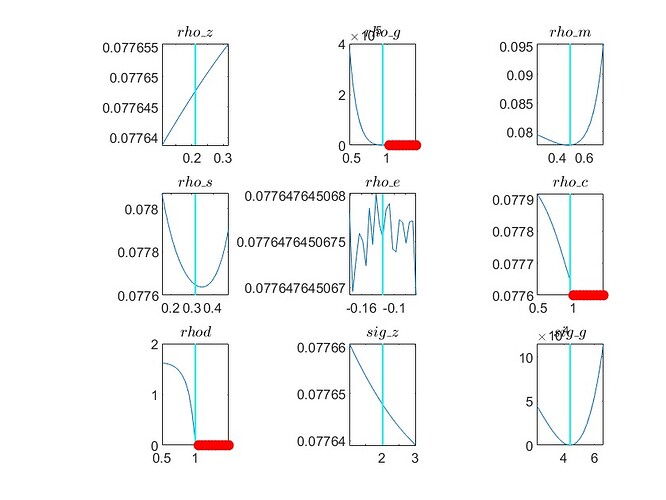
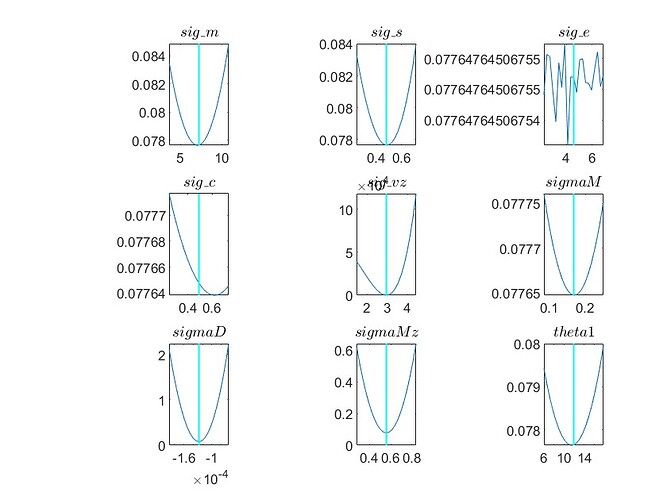
(6) Graph for Minimum Check Plots:

The plots for parameters like rho_z, rho_e, rho_c, rho_d, sig_z, and sig_e in my model appear unusual (please see the attached graphs). Do you have any advice on what might be causing these anomalies?

I have attached my code and log file for reference. Thank you very much for your time and assistance!

Best regards,
Ya

updated06051.rar (85.7 KB)

[jpfeifer]

1. @yw3864a

   How do I generally decide which parameters to include in the estimated_params
   for estimation?

   See

How to select parameters for estimation?

There is no hard rule. But it’s quite common to calibrate parameters that i) are not well-identified from the data and ii) where we have a good idea what the parameter value is. An example are the discount factor and the depreciation rate. They are often not well identified from cyclical moments but can often be set to to sensible values based on long-run averages for the investment to capital ratio and the long-run interest rate. The risk aversion parameter is another example. There is good mic…

2. Usually, you pick the moments that you are most interested in. That’s the difference to full information estimation.

3. It depends on whether nonlinearities are important. If higher order does not work, there is often a problem with the scaling of shocks (scaling by 100). Also, often pruning helps.

4. To compute the standard deviations, you need a positive definite Hessian at the mode. Looking at the mode_check pictures, that is not the case in your results, most likely due to a corner solution.

5. If your model is overidentified, the J test ist for testing whether the model is rejected by the data.

6. Enable options_.debug=true; to see where the dots comes from. But given that the autocorrelation coefficients go to 1 (unit root), you most likely have a problem with the observation equations. The mean of the data and the matched model variables most likely differ.

[yw3864a]

Thank you vey much. That’s very helpful!