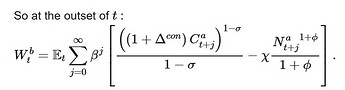Thank you for the reply!
(BACKGROUND)
Yes, I need conditional welfare in both the baseline and the alternative regime.
For the baseline, the Competitive Equilibrium (CE) scenario, it is indeed perturbed around its deterministic steady state, the concept that is also recently discussed in the thread:
For the Ramsey case, I’m not sure whether the economy is approximated around the Ramsey steady state or somewhere else, after all I don’t see Dynare’s report about this sort of steady state.
But this seems to be not important. Suppose Dynare can compute the true conditional welfare of the Ramsey. Then the merit of partial welfare is that it allows the Ramsey case and the CE case to be compared at the same initial point, probably CE’s deterministic steady state, if I understand the following equality correctly:
Anyway, I saw this expression almost everywhere, for example, in
Yet, his derivation is the same as the above JEDC paper, but the numerical part is not quite clear.
https://www.sciencedirect.com/science/article/pii/S0304393218304859?via%3Dihub
The authers compute the welfare in an optimal simple rules.
So it’ll be rather interesting to extend this approach in a Ramsey setting!