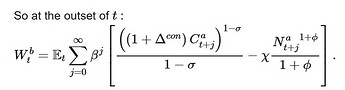Hello everyone,
I would like to ask questions related with welfare calculation under the optimal policy. My computation basically follows this paper:
Let me summarize the main steps:
Suppose we have a separable utility function:
W_t =\displaystyle \mathbb{E}_t\sum^{\infty}_{j=0}\beta^j\left[\frac{{C_{t+j}}^{1-\sigma}}{1-\sigma}-\chi \frac{{N_{t+j}}^{1+\phi}}{1+\phi}\right].
Specifically, in the baseline Competitive Equilibrium (CE) case, we define the conditional welfare:
W^b_t = W^{Cb}_t+W^{Nb}_t,
in which
W^{Cb}_t = \displaystyle \mathbb{E}_t\sum^{\infty}_{j=0}\beta^j\frac{{C^b_{t+j}}^{1-\sigma}}{1-\sigma}, and W^{Nb}_t = \displaystyle -\mathbb{E}_t\sum^{\infty}_{j=0}\beta^j\chi \frac{{N^b_{t+j}}^{1+\phi}}{1+\phi},
where C^b_{t+j} and N^b_{t+j}, for j = 0,1,\dots, are consumption and labour sequences when the economy achieves the CE.
Similarly, W^{Ca}_t and W^{Na}_t are the partial conditional welfare when the economy is in an alternative policy regime.
So at the outset of t:
\displaystyle W^b_t = \mathbb{E}_t \sum_{j=0}^{\infty} \beta^j \left[ \frac{\left(\left(1+\Delta^{con}\right)C^a_{t+j}\right)^{1-\sigma}}{1-\sigma} - \chi \frac{{N^a_{t+j}}^{1+\phi}}{1+\phi} \right].
Work out \Delta^{con} implicitly:
\displaystyle \Delta^{con} = \left[ \frac{W^b_t-W^{Na}_t}{W_t^{Ca}}\right]^{\frac{1}{1-\sigma}}-1.
Now my question is how to compute W^{Ca}_t and W_t^{Na} in a Ramsey context?
First, we know W^b_t under the CE can be derived by
oo_.dr.ys(W^b_t)+0.5*oo_.dr.ghs2.
Then according to the new functionality in Dynare 4.7:
If the alternative policy is a Ramsey type, by evaluate_planner_objective, we know W^a_t.
But how to split this value into two parts, W^{Ca}_t and W_t^{Na}?
Sincerely,
ToT