Questions about using log linearized equations in Occbin

General DSGE Modeling Replication Attempts
1

I have a set of log linearized equations from Eggertsson et al. (2019)

image
image1088Ă—888 77.4 KB

I typed the equations as it is on Dynare with model (linear).

For example,

model (linear);
Y = (chi*C_b_ss/Y_ss)*C_b + ((1-chi)*C_ss/Y_ss)*C_s;

Then the resulting output I get will be log deviations. I defined C_b_ss, C_ss, and Y_ss on the parameter block.

My questions are as follows.

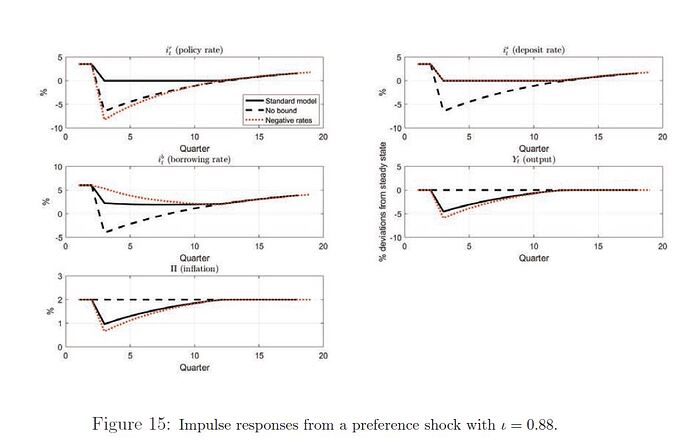
  1. Is it possible to get a figures like this (Figure 15 from Eggertsson et al. 2019) with my attached .mod files using Occbin? When using Occbin with my attached .mod files, I am able to get a graph for “No bound” but I am unable to get a graph for “standard model” and “negative rates”.

a2
a21035Ă—671 51.3 KB

  1. If so, how do you deal with constraints (Constraint, Constraint relax) for log linearized equations on Occbin?

Below is my attached .mod files. SYP_loglinear is for linear solution, SYP_loglinear_b is for getting piecewise solution. runsim_SYP_loglinear is my Occbin file.

SYP_loglinear.mod (2.6 KB) SYP_loglinear_b.mod (2.7 KB)
runsim_SYP_loglinear.m (3.3 KB)

Any help would really be appreciated.

Thank you

2

You did not provide information on which paper you are exactly dealing with and what
"No bound”, “standard model”, and “negative rates” are meant to denote. My guess is that “no bound” refers to a model without ZLB. You should obtain that picture by running the unrestricted mod-file without Occbin. “Standard model” seems to be the usual output from Occbin.

1 Like
3

Sorry Professor Pfeifer, I will clarify my question better in the future, if needed. Currently, I am so close to replicating the figure!

4

Dear Professor Pfeifer,

Sorry to bother you again… what does unrestricted mod-file mean? Is that just a regular mod-file without using Occbin?

Sincerely,

Eric

5

In case of a single constraint, Occin takes two mod-files as an input, one with the constraint binding and one where the constraint is slack, i.e. the respective variable is unrestricted. I am referring to running the latter file without Occbin.

2 Likes
6

Okay, I understood now. Thank you for your time professor.