Hi, everyone!
I have a question of the following equation’s log-linearization:
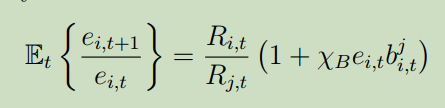
In the code, the equation like this:
de(+1) = r_h - r_f + chi_B*b;
de = e-e(-1);
Rit is r_h, and Rjt is r_f.
Could someone tell me the process of log-linearization?
Thank you very much!
Going step by step:
\begin{gathered}
{E_t}\left( {\frac{1}{e}\left( {{e_{t + 1}} - e} \right) + \left( { - \frac{e}{{{e^2}}}} \right)\left( {{e_t} - e} \right)} \right) = \hfill \\
\frac{1}{{{R_j}}}\left( {1 + {\chi _B}eb} \right)\left( {{R_{i,t}} - {R_i}} \right) + \left( { - \frac{{{R_i}}}{{R_j^2}}\left( {1 + {\chi _B}eb} \right)} \right)\left( {{R_{j,t}} - {R_j}} \right) + \frac{{{R_i}}}{{{R_j}}}\left( {{\chi _B}b} \right)\left( {{e_t} - e} \right) + \frac{{{R_i}}}{{{R_j}}}\left( {{\chi _B}eb} \right)\left( {{b_t} - b} \right) \hfill \\
{E_t}\left( {\frac{e}{e}\frac{{\left( {{e_{t + 1}} - e} \right)}}{e} + \left( { - \frac{{{e^2}}}{{{e^2}}}} \right)\frac{{\left( {{e_t} - e} \right)}}{e}} \right) = \hfill \\
\frac{{{R_i}}}{{{R_j}}}\left( {1 + {\chi _B}eb} \right)\frac{{\left( {{R_{i,t}} - {R_i}} \right)}}{{{R_i}}} + \left( { - \frac{{{R_i}{R_j}}}{{R_j^2}}\left( {1 + {\chi _B}eb} \right)} \right)\frac{{\left( {{R_{j,t}} - {R_j}} \right)}}{{{R_j}}} + \frac{{{R_i}}}{{{R_j}}}\left( {{\chi _B}b} \right)e\frac{{\left( {{e_t} - e} \right)}}{e} + \frac{{{R_i}}}{{{R_j}}}\left( {{\chi _B}e} \right)b\frac{{\left( {{b_t} - b} \right)}}{b} \hfill \\
{E_t}\left( {{{\hat e}_{t + 1}} - {{\hat e}_t}} \right) = \frac{{{R_i}}}{{{R_j}}}\left( {1 + {\chi _B}eb} \right)\left( {{{\hat R}_{i,t}} - {{\hat R}_{j,t}}} \right) + \frac{{{R_i}}}{{{R_j}}}\left( {{\chi _B}eb} \right)\left( {{{\hat e}_t} + {{\hat b}_t}} \right) \hfill \\
\end{gathered}