Hi, dear professor, I want to such a thing and wonder if it possible to realize it in dynare.
First I do Bayesian estimation and have the smoothed shocks in my hand.
and I change the basic model to a ramsey-policy or a OSR style that makes certain policy variable optimally determined.
And then I put the smoothed shocks into the new ramsey-policy or OSR model in order to get the counterfactual smoothed time path of some certain endogenous variable.
So is that possible?
I know if I just change some part of the model, I could use simult_.m file to do that.
That should in principle be possible. The challenge may be to set the initial Lagrange multipliers. But of course, you can start everything at the steady state.
Thanks a lot. what I refer to is the linearized model so the steady-state is the same.
But how could I achieve that?
should I follow your replication MOD of Jerman&Quandrini(2012), and directly use the simult_.m file?
And in that process, in which step should I call the ramsey_policy.m file?
Note that I just wanna to use dynare’s own ramsey_policy calculation, not do it by hand myself with numbers of Lagrange multiplier.
Thanks.
You will have to do this in two separate files. The first one does the estimation. The second one does the Ramsey policy for the same model and conducts the simulation using the simult_-function. That’s where you will need the Lagrange multipliers.
Thanks, dear professor.
I still do not know in your so-called “The second one does the Ramsey policy for the same model”, whether I could directly use Dynare’s own Ramsey-policy command, or I should calculate the social planner’s F.O.C by hand and put it into the model?
Thanks for answering!
You should use Dynare’s ramsey-routines in the second file.
Like in Stéphane Adjemian’s paper, they start the simulation from the steady-state for each model? I tried using simult to do a similar task in this thread and in that paper. But then, I face a problem because I do not have y0 (initial state for the variables in the Ramsey policy model).
You should have the initial states for the original model variables. All you then need to set is the Lagrange multipliers, typically to 0.
Thanks!!! May I ask one last question?
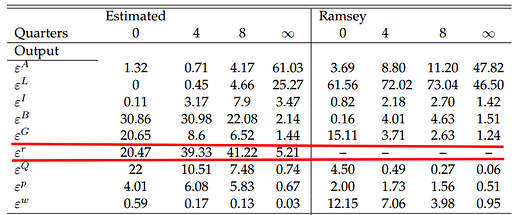
- In the original estimated model, we have monetary policy shocks. Together with the other shocks, which can replicate the data.
- But in the Ramsey model, there is no monetary policy shock…but rather cost-push shock together with the other shocks.
Thus, the shock structure in the original and Ramsey model is not the same. So how can we use the estimated shocks from the original to simulate macroeconomic variables under Ramsey policy as mentioned in Stéphane Adjemian’s paper? Replace cost-push shock (in Ramsey) with monetary policy shock (from the estimated model)? How does it work? Thanks!!
My guess is that you do not use the shocks of the estimated original model, but rather re-run the Kalman smoother on the data for each model at hand.
One can do that for a Ramsey model? Also, won’t that suggest that in each model, you will just get back the data?
In Adjemian’s paper, it appears though that the shocks are estimated outside the Ramsey model from this quote, “Given the estimated structural shocks, we simulate the path of the main macroeconomic aggregates under the Ramsey policy”.
Let me also say thanks for the replies. Really helpful.
- My mistake. The Kalman smoother is about decomposing the observables, which was not done here.
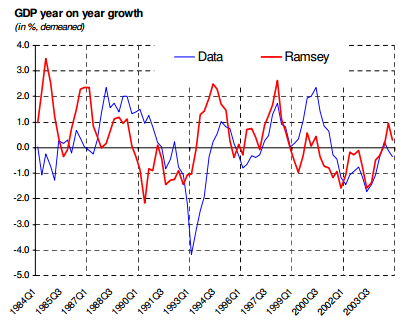
- What the paper seems to do is a counterfactual: how would output have looked with the same shocks, but with optimal monetary policy. In that case, it of course makes sense to have no monetary policy shocks. After all, they are policy mistakes a Ramsey planner would not make.
So like replace monetary policy shock with a constant. And then simulate the macroeconomic variables under Ramsey policy. I replace it with a constant because I have a cost-push shock in the Ramsey model…so that there is an equal number of shocks in the original model and the Ramsey model.