Dear all,
I built a DSGE model. When I use monetary policy rules ‘ r = kappa_r * r(-1) + ( kappa_y * y + kappa_pi * pi) + mu_r’ , dynare code can run . I want monetary policy to respond to leverage, so monetary policy convert to ‘ r = kappa_r * r(-1) + ( kappa_y * y + kappa_pi * pi) + kappa_lev * lev + mu_r’. When reaction coefficient kappa_lev equeal to 0.2,the code aslo works. But when equal to other values,it shows “Matrix must be positive definite with real diagonal.”
I don’t know what the problem is?Can someone help me find out why? Thank you in advance.
data.xls (33 KB)
price.mod (10.6 KB)
This means that the posterior mode optimizer ended up on a point in the parameter space which is actually not a local maximum. Hence you did not really obtain a mode. You need to change the starting point for the optimizer, or use another optimization algorithm.
Search the forum for “hessian not positive definite” for more examples of similar situations.
Try mode_compute=5
sebastien, I’m sorry I don’t understand your meaning of this sentence ‘Hence you did not really obtain a mode’. Is there a problem with my model or with my estimates?.Could you explain a bit more in detail about it. I’m really sorry I don’t know much about dynare’s optimization algorithm.
jpfeifer,thanks a lot. It seems work well on mode_computer=5.
So here comes a question, when I make an estimate,which mode_computer should I choose to fit the model better?
At Code to loop over different dynare optimisers
you can find some code to loop through several optimisers available in dynare.
Cheers
Reuben
Concerning the optimization algorithm: what Dynare does first during estimation is to maximize the posterior density, in order to find the posterior mode.
For that purpose, Dynare uses a numerical optimizer (there are several such optimizers available, whose selection can be done through mode_compute).
In practice, there are two problems which are common to all those algorithms.
The first problem is these algorithms can only find a local maximum of the posterior density. It is impossible in the general case to be sure that they have found a global maximum (except in some special cases, for example if your posterior density is globally concave).
The second problem is that these algorithms can fail to converge, in the sense that they will end on point which is not a local maximum. In this case, the hessian matrix of the posterior density at the given point will not be negative definite (which it ought to be, if the point was a local maximum). This is the situation which you encountered here (note that Dynare was talking about non-positive definite matrix, because it is actually looking at the opposite of the density).
sebastien, thanks for your detailed explanation. I’m trying to understand it.
jpfeifer,thank you very much, the problem of Bayesian estimation should be solved. After solving the problem of Bayesian estimation.The other results seem to be correct, except for inflation.
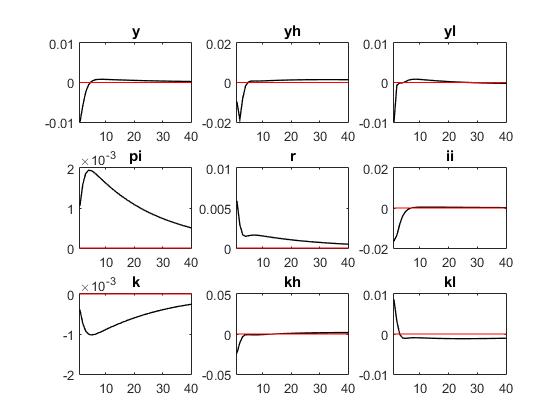
Why does inflation grow after monetary policy shocks? Did I make a mistake somewhere? is it possible to tighten monetary policy to raise inflation?
data2018.xls (31 KB)
price.mod (10.7 KB)
Have you tried to use an iid monetary policy shock? I have noticed these strange IRFs (in the standard 3 equation NK model) when the monetary shock is very persistent. Perhaps aggregate supply contracts to a greater degree than aggregate demand and puts upward pressure on prices…
What is your estimate of rho_r ?
Cheers
Reuben
Reuben, thank you for your cue. I have iid monetary policy shock ‘mu_r = rho_r * mu_r(-1) + eps_r;’ and ‘rho_r,beta_pdf,0.5,0.2;’ rho_r is equal to 0.5. Am I right? I don’t know where I was wrong.
what do you get when you estimate rho_r? 0.5 is just the prior, right?
Yes,0.5 is just the prior. Estimated results of rho_r is ‘rho_r 0.500 0.2902 0.2173 0.3921 beta 0.2000’. Problems still exist.
set rho_r = 0 without estimating it and check irf.