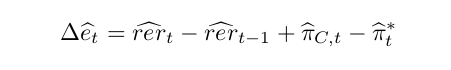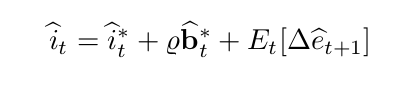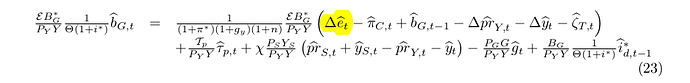Hi everbody,
I am trying to replicate the SOE developed by Liu (2006): A small new keynesian model for the new zealand economy in dynare, so that eventually I will be able to estimate it for Malta. However, while I was able to replicate the model and IRFs using Uhlig’s Toolkit, Dynare is giving me the following errors:
There are 4 eigenvalue(s) larger than 1 in modulus
for 5 forward-looking variable(s)
The rank conditions ISN’T verified!
??? Error using ==> print_info
Blanchard Kahn conditions are not satisfied: indeterminacy
Error in ==> stoch_simul at 44
print_info(info, options_.noprint);
Error in ==> Liu_replica at 212
info = stoch_simul(var_list_);
Error in ==> dynare at 125
evalin(‘base’,fname) ;
Any help on how to resolve this issue? Why are the BK conditions not satisfied in Dynare when no such problems were identified with Uhlig’s toolkit?
Eventually, I will have to adapt the model for a country that’s in a monetary union (fixed exchange rate regime). As a result, the interest rate will be determined exogenously rather than set by the home central bank via a Taylor Rule. Any ideas on how to do this?
Liu_replica.mod (4.47 KB)
Liu_2006.pdf (861 KB)
Hi,
this is a dynare timing convention issue associated with the real exchange rate (q) in the model;basically you can’t use the same timing as in that paper. but it should work if you add the instruction “predetermined_variables q;” or change directly its timing by lagging “q” of one period.
Best
When I’ve use the command ‘predetermined_variables’, the following error appeared:
??? Undefined command/function ‘predetermined_variables’.
Error in ==> Liu_replica at 152
predetermined_variables q;
Error in ==> dynare at 125
evalin(‘base’,fname) ;
The model worked when I lagged the real exchange rate (q) by 1 period but the IRFs were different from the original paper, both qualitatively and quantitatively!
Any help on how to solve this issue?
To be sure, I’m using dynare version 4.1-alpha1
thats curious… because this instruction works for me (see the attached file)
Best
NB: I use the latest version of dynare
Liu_replica.mod (4.5 KB)
Hi, could you provide some intuition as to why the real exchange rate is a predetermined variable? It makes sense that capital or Bonds are predetermined in such models as they are determined already in the previous period (end of period notation). Why does this by convention apply to the real exchange in Dynare, when this variable is for example contemporaneously influenced by monetary policy?
I have downloaded the latest version and the IRFs are still qualitatively and quantitatively different from those of the original paper. So there must be something else that I’m missing with Dynare code (although, as I’ve said before, the same equations with Uhlig’s toolkit works fine!). Any insights on why?
I would also appreciate if you expand further on why the real exchange rate should be considered a predetermined variables.
There is something weird with the paper. The Appendix lists 14 equations but there are only 13 variables. This forces you to combine the Euler equation and the international risk sharing equation but there is no theoretical grounds to do so.
Also, on page 15, the author lists pi_h in y, among “other endogenous variables”, but pi_h appears with a lag in the model.
If you want to understand why Dynare and Uhlig’s Toolkit give different results, you should
- compare the eigenvalues. If the eigenvalues are different, there is a difference in the models that you entered in both program
- if the eigenvalues are the same, you should verify the Blanchard and Kahn condition by comparing the number of explosive eigenvalues and the number of forward looking variables.
Best
Michel
Does this mean that the comment about the predetermined exchange rate is obsolete and there is something else wrong?
Permit me to revive this thread on predetermined exchange rate.
I have encountered a timing issue myself where the mod file only runs if I make the exchange rate predetermined. But this is wrong according to the discussion here as there is no intuition as to why the exchange rate should be predetermined and it is, moreover, not a timing convention in dynare.
I was reading this paper (THE CHILEAN BUSINESS CYCLES THROUGH THE LENS OF A STOCHASTIC GENERAL EQUILIBRIUM MODEL) where a predetermined exchange rate appears in the equilibrium equations of the model via a law of motion equation for the exchange rate.
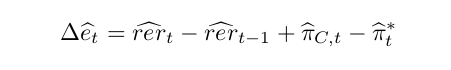
Tracing this back in the model, a predetermined exchange rate appears in the fiscal rule equation of the model by assumption, which I think will vanish when this equation is simplified.
So, tractability seems to be the reason why predetermined exchange is in the model…my guess though.
Nevertheless, the exchange rate timing in the other equations of the model (for example, UIP) does not change, so yeah, we cannot simply lag the exchange rate to make the mod file run in dynare.
If anyone has yet found a reason why the exchange rate may be predetermined, I would be happy to know. Many thanks!!
Hi
The first equation in your post is merely the definition of the real exchange rate. of course, in terms of changes rather than in levels.
If you write the UIP equation (which is forward looking) in terms of the real exchange rate instead of the nominal exchange rate, and do the same with the other equations, the real exchange rate will not look like it is predetermined.
Reuben
’
1 Like
Hi Jacob, here is the log linearized UIP:
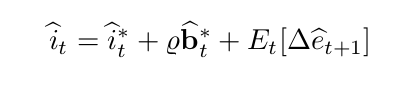
It doesn’t seem like the real exchange rate will be predetermined in the UIP. At least I cannot see how…It looks like we will have rer(+1), rer, and rer(-1) in the model. Does this mean rer is both forward-looking and predetermined? I will search for the replication mod file to confirm though…I saw something like that on MMB website.
And here is the log-linearized fiscal policy rule where rer and rer(-1) can replace Δe:
Having a past exchange rate showing up somewhere does not mean that the exchange rate is necessarily predetermined. As pointed out above, it can show up due to definitions.
2 Likes
Hi
Like Johannes mentions, just because a lag of the variable appears in the model, it does not necessarily make it predetermined in the sense we say financial assets or the capital stock is predetermined in the primitive optimisation programmes.
Typically, in these open economy models, people rewrite the equations in terms of relative prices such as real exchange rates and terms of trade or the relative price of imports w.r.t domestic output price…That is because these relative prices are stationary, whereas the level of the nominal exchange rate or any absolute nominal price level for that matter, are not stationary. The NK model does not pin down the steady-states of the price level or the nominal exchange rate. So the log-deviations of these variables will not return to 0 after a shock.
However, the change in the nominal exchange rate (delta e_t in your equations) is stationary, just like say, inflation is stationary while the price level is not. That explains why the delta e_t appears in your second equation ( I suppose the govt bonds are foreign-currency denominated in that model).
1 Like