Hello everyone,
I am estimating a model, for all the parameters the posterior distribution looks good, with a smooth shape and no flat areas or strange things, the trace plots look decent too, however, when it comes to a single parameter the posterior distribution and a prior coincide exactly, but it only happens with that parameter, does that mean that the whole estimation is wrong? Can the estimation result be considered valid?
I have reviewed quite a few papers and they tend to omit the prior-posterior graphs, and in some cases if these graphs are included, the coincidence of both distributions does not seem to be so important for the conclusions, is it really a problem, for example, to publish an article?
I attach some images of the parameter
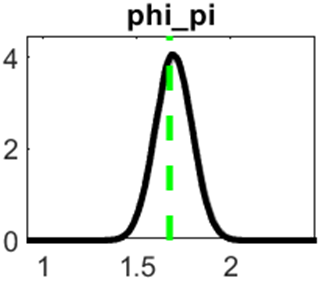
This one parameter is almost surely not identified. Generally, that is a problem.
Thanks for your reply
then could it be said that the estimation is somehow incorrect or invalid for all the other parameters?
It means the data does not help to pin down that one parameter. If the value chosen with the prior is “incorrect” this will affect the estimated parameters as well. I would try to fix this issue.
Thank you again for your help
I solved the problem partially, I ran the identify command and all the parameters are identified, the problematic parameter is \phi_{\pi} which is the central bank’s response to inflation, just two quick questions
-
I got a posterior distribution somewhat different from the prior distribution (not very different, but at least not the same as in the image above) by adding inflation measurement errors, is it usual to solve this problem by adding measurement errors? or was it coincidence?
-
In general, I see that in the literature it is usual that the data does not provide much information to identify the parameter \phi_{\pi}, an example is in ALLV (2007), is there any particular reason why this can happen in SOE models? I attach an image of the ALLV example and my model (they are quite similar although the model is not the same and the data is for totally different economies)
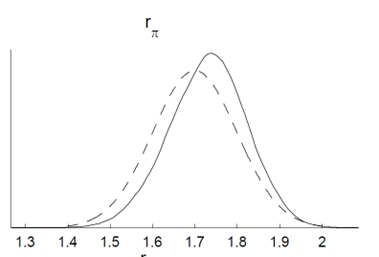
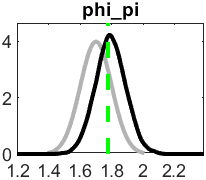
Best regards
Without the files, it is impossible to tell. But it’s strange to have all parameters identified and still identical priors and posteriors.
- I don’t think measurement errors are a solution to your problem.
- You did not attach anything. But having parameters weakly identified is not unusual. Having them completely unidentified would be a problem.



