As I know, the response of a variable X_t (to a particular shock) is persistent when it takes a long time for it to return to the steady-state.
But when the response of X_t quickly crosses the steady-state or zero line, and after that takes a long time to return to zero, is it still persistent? Or we say it is persistent only from the point where it crosses the steady-state line?
This is tricky. The term “persistence” does not have a clear definition. You could most probably conceptualize it as the absolute value of the largest eigenvalue of the companion form.
You seem to have an AR1 in mind where the speed of return to 0 uniquely determines this eigenvalue.
For higher order processes it’s not as clear, because there may be overshooting. But if the return to steady state after that overshooting still takes a long time, this indicates a large eigenvalue and a lot of persistence.
So if I have 2 models and the only difference is that one has habit formation and the other does not. I should expect larger eigenvalues for the model with habit formation relative to the model without habit formation, right?
I know I have deviated a little bit from my initial question, now I am asking about persistency in the model, not just a single variable.
Usually, the answer is yes. With perfect habit formation, you should have a unit root.
Hi prof. Pfeifer, may I ask this question.
If model1 has higher persistence (measured by the modulus of its largest eigenvalue) relative to model2, it does not necessarily mean all IRFs of model1 will be more persistent than that of model2, right?
I simulated the general solution of some dynamic system with two different set of eigenvalues. And indeed, the model with the largest eigenvalue in absolute terms (model1) is more persistent. But these are not IRFs.
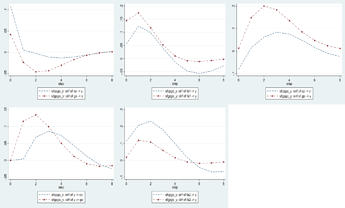
I built two different VAR models (second figure attached) for two sectors. Only data changes, but same model.
Modulus of the largest eigenvalue of the model with BLUE IRFs is 0.809.
Modulus of the largest eigenvalue of the model with BROWN IRFs is 0.708.
I was kinda expecting BLUE IRFs to be relatively more persistent for all shocks in the model. But that appears not to be the case.
Many thanks for you comment!!
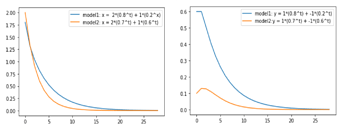
SIMULATED DYNAMIC MODEL
model 1: \lambda (eigenvalues) = 0.8, 0.4
[x_t, y_t]' = 0.8^t [2, 1]' + 0.4^t [1, -1]'
model 2: \lambda(eigenvalues) =0.7, 0.6
[x_t, y_t]' = 0.7^t [2, 1]' + 0.6^t [1, -1]'
VAR model
Consider stacking a set of independent AR(1)-processes into a VAR. That largest eigenvalue will be the largest AR(1)-coefficient. But that AR(1)-coefficient will only be relevant for one of the shocks. That shows you that the IRFs to individual shocks are not necessarily affected by all eigenvalues.
Many thanks!!
So it appears we cannot connect the persistence of a linear system (as measured by the largest eigenvalue of the companion matrix) to something that is true for all equations in the system, right? Like IRFs and forecasts, since the effect of a higher or lower system persistency will be relevant just for one equation in the system.
Sorry for dragging this…:). I think I understand persistence now by definition. But actually struggling to find its implication on the results of a DSGE or VAR model.
I read this paper, and the authors say something like if persistence of a linear system is underestimated, “forecasts revert to the unconditional mean too quickly”. So it appears this is some general result for all the equations in the linear system since ‘forecasts’, as used here, is plural. But then IRFs and I guess forecasts of each equation are not necessarily affected by the largest eigenvalue, right?
Maybe you have a comment on the implications of higher persistence on the results of a multivariate linear model, like the DSGE or VAR model.
I know the homogeneous solution of a difference equation is like the dynamics/fluctuation of the variables (in the model) around the steady state (i.e., the particular solution). But since there are no shocks here, can I say the evolution (over time) of variables in a high persistence model reverts back to its mean relatively slowly.
The problem is that your equations are coupled, but then you are only interest in the effect of an impulse to one equation and how it affects individual variables over time. I am not aware on general rules how to measure the persistence for these cases easiyl.
1 Like
I think I found one general rule. If I extend the number of steps of the IRFs to say 20, all IRFs in the model with a relatively larger eigenvalue dies out slowly (i.e., they have more oscillations) over time although it may be the first to cross the zero line after a shock in some cases.
Before I conceptualized a high persistent IRF as reaching the steady-state line relatively slowly. But I guess I was wrong. Rather it should be conceptualized as which IRF dies out relatively slowly. Thus, it may reach the state-state quickly but dies out slowly, suggesting higher persistence.
Indeed, persistence is about how fact you go back to the steady state in the long-run, not when you hit it first.
Hi Prof. Pfeifer, may I kindly ask something.
I compared the persistence of two models: RBC with habit formation (model1) and RBC without habit formation (model2). Visually, the IRFs in model1 are more persistent as expected.
But in case I want to compare persistency using the eigenvalues of the two models, then I should just focus on the modulus of the largest stable eigenvalue, right? If I do that, the results are consistent with the visual examination of the IRFs.
Yes, the unstable eigenvalue are for ruling out indeterminacy. In fact, it’s about the eigenvalues of the Kalman transition matrix A:
%get state indices
ipred = M_.nstatic+(1:M_.nspred)';
%get state transition matrices
[A,B] = kalman_transition_matrix(oo_.dr,ipred,1:M_.nspred,M_.exo_nbr);
1 Like
Many thanks!!! It appears though that a small change in the largest eigenvalue, say, from 0.95 to 0.96 actually reflects a big change in persistency. That is interesting…
Consider the half-life
log(0.5)/log(rho)
For 0.95 it’s 13.5, but for 0.96 its already 17.
1 Like