Hi everyone,
Is there a way to do permanent volatility shock?
z = rho*z(-1) + e * omega;
Basically I want to run a simulation on two regimes, high volatility and low volatility regimes. I can do this separately; like run one simulation on a low volatility and run another simulation with high volatility. But I am wondering if I can do both in one simulation?
What exactly is the experiment you have in mind? It seems you want to conduct a simulation where there is a one-time permanent shock to volatility. As always, there is the question about the assumed information structure. Do agents know that volatility can change and take the into account? The problem is that if volatility follows a random walk, i.e. there are permanent shocks, then no finite solution may exist.
For that reason, you may have to consider true regime-switching model.
1 Like
Yes, that is exactly the experiment that I want to run.
The agents do not know that there will be a permanent shock.
Then the next question is which type of IRF are you after? If you do IRFs at the stochastic steady state this may be feasible by simply introducing a unit process for the volatility. That would be problematic for GIRFs.
I actually found your Risk Matter Dynare code.
I also found a few other old discussion about this.
Basically, I have to use order 3, with pruning, and at least 20,000 replication.
The problem is not about how to implement this. GIRFs are straightforward. The question is whether this will work. Keep in mind that a unit root implies that simulations will wander arbitrarily far away from their starting point. That may be a huge problem for GIRFs.
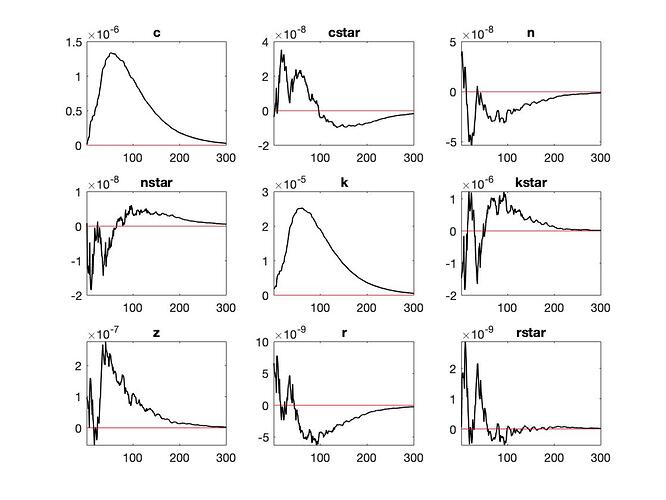
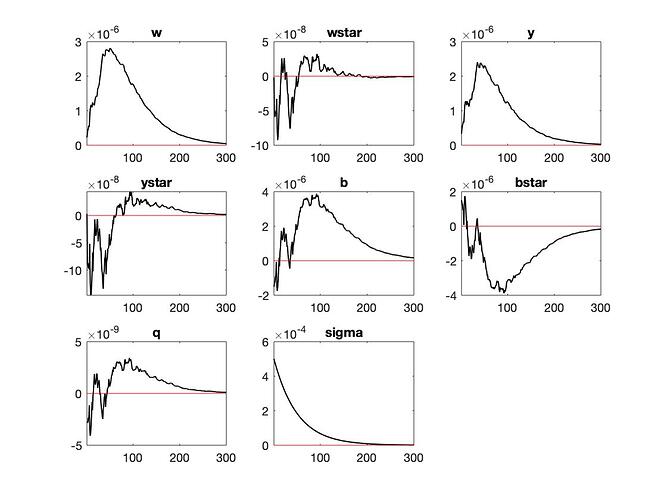
By having a shock to both the TFP and the volatility of the TFP, this is what I got
I decided to not have a permanent shock.
I used around 5000 replications, should I do 20,000 instead or higher?