Hi,
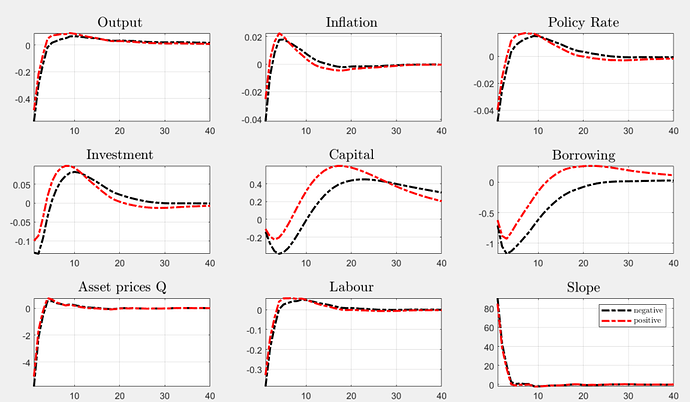
I built a very simple model with an occasionally binding constraint implemented through a penalty function as in Brzoza Brzezina et al. (2013). I am plotting IRFs with order = 2 and comparing a positive with a negative shock to look at the asymmetry, but for some reason both shocks look contractionary. Any chance you have an idea of what I am missing?
Many thanks
Manuel
test_250624.mod (4.1 KB)
test_250624_steadystate.m (1.9 KB)
How did you generate the graphs?
the command is:
stoch_simul(order=2 ,irf=40, pruning);
to distinguish between positive and negative shock I changed the sign of the exogenous variable here:
mb = (1-rhob)STEADY_STATE(mb) + rhobmb(-1) + eb;
You did not provide the m-file called in the steady state file.
Sorry about that. It is now attached. Many thanks
root210624.m (760 Bytes)
There is something about asymmetry that kicks in for large shocks. If you try
var eb = 0.0001;
you will get the expected asymmetry.
Yes, thanks. Perhaps could this be due to pruning? I read pruning it is not very efficient at approximating penalty functions. However, without pruning even a 0.01% shock is too large and IRFs are explosive.
That may well be. I am not sure how well your strongly nonlinear model will perform with perturbation solutions.
Yes. Indeed, if I replicate Zacek (2020) for example, it seems clear that with pruning and order =2 the penalty function is not very well approximated. However, if I remove pruning, the path is explosive and I cant seem to be able to run shocks of the size parametrized in the paper (0.005, 0.006, 0.002). That makes me wonder how IRFs are built in these papers?
Manuel
root270624.m (1006 Bytes)
Zacek_2020_steadystate.m (1.8 KB)
Zacek_2020.mod (4.2 KB)
Without the codes it is impossible to tell. Maybe they used IRFs at the stochastic steady state instead of generalized IRFs tracing the ergodic distribution. Those are almost never explosive.
I see, many thanks. Are you aware of any codes publicly available to compute those?
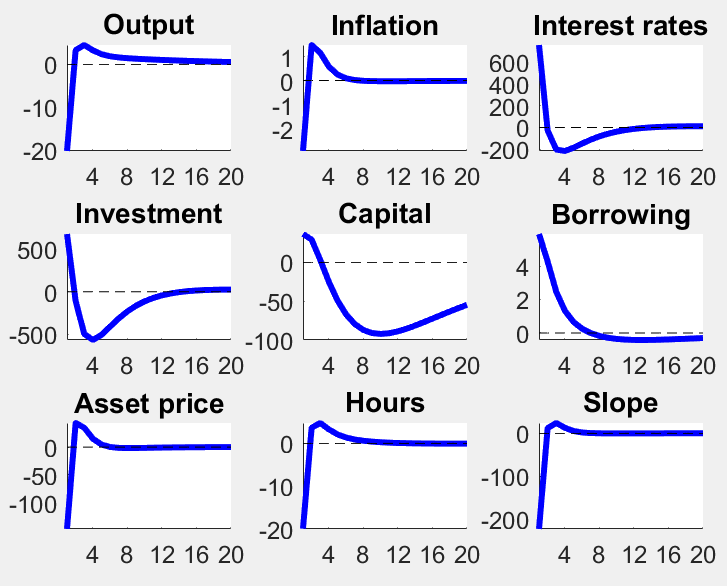
Many thanks. I gave it a try, but for some reason when the shock hits at the stochastic steady state (after the burnin period) it has an extremely large impact that I cant explain. Also, if I remove the pruning option the model is again explosive, and therefore can’t compute IRFs.
Are you sure your shock scaling is correct?
Sorry, this is the code I used.
test_280624.mod (7.9 KB)
test_280624_steadystate.m (1.8 KB)
root270624.m (1006 Bytes)
you are right, sorry, in the example with pruning the mistake is the size of the shock.
The numbers in sqrt(.) however correspond to lower stdevs than those in the paper, and if you increase them accordingly it is still explosive. but the code was very helpful, many thanks.
test_280624.mod (8.2 KB)
test_280624_steadystate.m (1.9 KB)
root270624.m (1006 Bytes)
When I run your files, I get an error message that the steady state file is incorrect:
Residuals of the static equations:
Equation number 1: lambdap : 0.000000
Equation number 2: 2 : 0.000000
Equation number 3: 3 : 0.000000
Equation number 4: 4 : 0.000000
Equation number 5: Y : 0.000000
Equation number 6: psib : -73516.854378
This one should work I guess?
test_010724.mod (8.4 KB)
root010724.m (1006 Bytes)
test_010724_steadystate.m (1.9 KB)