Ask everyone. I encountered some confusion in learning Bayesian estimation. How to set the prior distribution parameters of Bayes, such as prior mean and variance. Is that a guess? There’s some quantitative studies that need to be done. Parameter estimation Are the parameter values that need to be guessed before estimation written in the parameter block? After the parameters are estimated, then rewrite the parameters into the mod file? Do the impulse response again? Thank you for the teacher’s advice, I am a beginner, more confused.
Hi heroluotao,
is this a technical question regarding how to enter prior mean, variance, etc. into Dynare or a theoretical one on how to find these terms? I will try to answer them both.
I start with the theoretical one. Following the wording of prior distribution we already see that this is something that we as researchers should/could have prior knowledge about. That could for instance be the domain of a parameter and where we believe the parameter will be. This stems from the definition of Bayes’ rule on which Bayesian estimation is built, I recommend looking up those terms in a textbook. That we are able to include prior knowledge into our estimation routine, through choosing particular prior distributions is one of the major distinctions of using Bayesian methods over frequentis ones like OLS and GMM.
Thus, you can put in your prior knowledge by choosing a particular prior distribution. There is, of course, literature on what distributions (Beta, Normal, Inv. Gamma) to use on which parameters, but in general it is up to you.
For Dynare, before you try to do estimation you should make sure your model runs in calibrated form. Only then you can start thinking about estimation, because there is a lot that can go wrong, starting from data treatment, observational equations, and mode finding to what exact algorithm to use.
But let’s give an example on how to include a parameter to be estimated into Dynare. Assume that you think that the parameter that governs the central banks reaction to output growth is called phi_y and your prior knowledge, based on theory and data, is that is follows roughly a normal around 0.1 with some variance (in the following case 0.15). Then, under estiamted_params you enter
phi_y , normal_pdf , 0.1, 0.15 ;
But again, you should do a lot of reading before approaching estimation. A good book is Bayesian Estimation of DSGE Models by Herbst and Schorfheide. Before writing too much, which maybe you are familiar with, I end it here and feel free to ask follow up questions.
But let me quote Prof. Pfeifer’s usual response here that he already posted in one of your other topics:
You are not supposed to work on estimation without intense supervision or sufficient prior training. I have seen too many cases like this miserably fail. Most of the time, the goals set are too unrealistic given the prior training and the time frame envisioned.
Dear DoubleBass, thank you so much for answering, I feel very productive
See also
Thank you professor Jpfeifer
Dear DoubleBass, after bayesian parameter estimation, if the parameter estimation is to be trusted. Whether to place the estimated parameters in the DSGE model instead of the original prior setting.
Dear jpfeifer , after bayesian parameter estimation, if the parameter estimation is to be trusted. Whether to place the estimated parameters in the DSGE model instead of the original prior setting.
I am not sure I understand the question. The whole point of estimation is to update the prior.
dear jpfeifer.I mean, when use Bayesian estimation, when the posterior mean and variance (posterior distribution) are estimated. Is it necessary to replace the original prior mean with the posterior mean? And then we do the impulse response
I think what you want to do is to do IRF-analysis awith the estimated parameter-values, right? If yes, there are two ways. One is to include bayesian_irf in the estimation command, which gives you IRF’s from the posterior distribution. Another way is to use, as I think you were saying, the posterior means and recalibrate the model and do ‘normal’ stochastic simulation IRF’s.
Dear DoubleBass, thank you very much for your answer
Note that Dynare will set the parameters to the estimated values after estimation. So running stoch_simul subsequently will used the updated parameters.
Thank you very much Professor Jpfeifer for your answer
I have a follow up question in regards to setting priors in relation to the initial parameterisation/ calibration.
Say I want to estimate all or some the parameters in the model, and for example Beta is usually set to 0.99 in the literature, does this implicate I should set the mean of the prior to 0.99 as well? Could I specify it like
beta, beta_pdf, .5, .1;
or will this lead to misspecification? I have not seen researchers initial calibration in papers, just the specification of the priors used, so I’m a bit confused.
Also, I have similar reflections as how to specify the shocks in the shock-block and the following estimation of their stderr in the estimated_params-block.
A beginner guide of these topics would be highly appreciated! Thanks.
Calibration is different from estimation. You need to decide what to do. It is usually a good idea to plot the prior.
beta, beta_pdf, .5, .1;
would imply a very strange shape for the prior, with you assigning the highest probability (mode) to 0.5.
Hmm, I’ve seen priors like that in papers. Anyway my questions are
-
Do researchers usually set the mean of the prior close to/ same as the initial calibration?
-
I’m a bit confused regarding the specification and estimation of the stderr of the shocks. For example, is this a correct specification?
shocks;
var eps_y; stderr 0.1;
end;
...
estimated_params;
stderr eps_y, inv_gamma_pdf, .5, inf;
end;
I’m asking so I haven’t missed something obvious. Thank you for your time and support, highly appreciated!
Hi everyone, I have a question related to this thread. I am estimating the Calvo parameter (theta) and coefficients in the Taylor rule. For theta and phi_pi, the posterior mean was always to the left of the prior mean after estimation, so I kept resetting the prior mean, moving it to the left until I got close to the theoretical lower bound (i.e., zero for theta and one for phi_pi). For phi_y, the posterior mean was always slightly to the right of the prior mean after estimation. So I have been increasing the prior mean for phi_y, but there is no theoretical upper bound so I have stopped at 3. 3 because that is the upper bound for this parameter in smets and wouters. What would you advise? Am I doing the right thing? Let me also add that log data density increases as I increase prior mean for phi_y.
For phi_pi and phi_y, maybe I can estimate OLS taylor rule and use the coefficients as priors and set the boundaries based on those estimates.
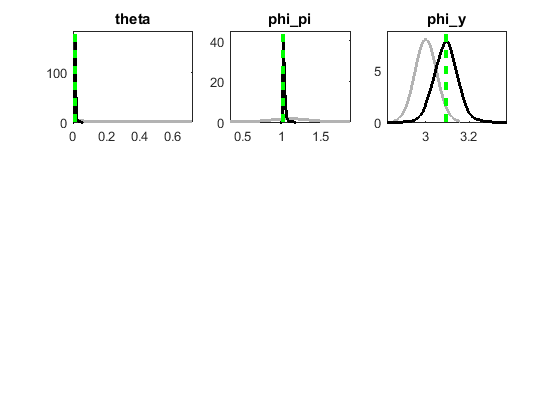
And for theta, there is one paper for my country that says, “The average frequency of changes is 93.72% meaning that prices indexes change almost every month in a year.” So theta close to zero is kind of consistent with this result. The effect of monetary policy shock on real variables is also small after estimation of my model which is consistent with other non-DSGE papers have also found that monetary policy is not effective for this economy.
Some other problems.
In the calibration version, after contractionary monetary policy, interest rate increases, and output and inflation falls. But after estimation, after contractionary monetary policy, all three variables fall…suggesting a strong feedback from the inflation rate and output to the interest rate.
Not sure how to interpret that feedback. It seems to suggest the CB changes interest rate at least twice in a quarter. But in reality, CB changes interest rate only once in a quarter, right?
Any comment on these issues will be very well appreciated. Thanks.
It is not correct to adjust a prior based on estimation results. Priors are supposed to capture information about the parameters before seeing the data. See e.g. Construction of priors using the data - #2 by jpfeifer