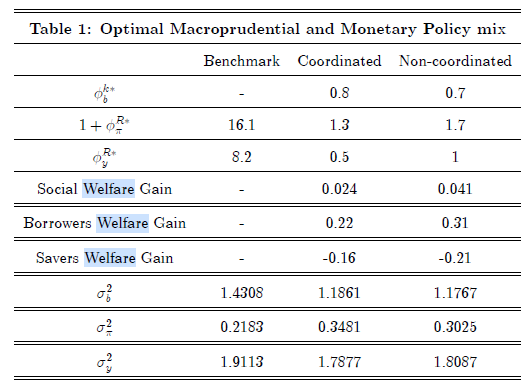
I want to analyze the welfare effects of macroprudential policy/monetary policy and want to replicate the welfare analysis and optimal policy mix between macroprudential and monetary policy done by Rubio and Carrasco-Gallego (2014)
Here, the loss function is defined as
L= var(pie) + lambda_Y*var(Y) + var(B)
B being the variability of borrowing, and Lambda_Y, the relative weight of the central bank to the stabilization of output.
I want to replicate Table 1, where they compare
- Benchmark: optimal parameters of the Taylor rule for monetary policy, assuming that
there is no macroprudential regulator. - If the central bank and the macroprudential regulator coordinate, they would aim at jointly minimizing the loss function each one with its own instrument.
- Both authorities act in a non-coordinated way.
Being very new to Dynare and Matlab, I am not 100% certain how to go about modeling this. I have all the structural equations set up (following Gerali (2010) two-type HHs (patient, and impatient (borrowing constraints) with nominal rigidities, financial frictions and monopolistic banks).
So I should add the loss function in my .mod file
l=var(pie)+ phi_y*var(Y) + var(B)
and how should I proceed from this? Any help will be very much appreciated!