On Optimal poliy parameters

[alexfra1709]

Dear professors,
I have a few questions about conducting optimal policy analysis. I am just a beginner at doing this excercise. I have tried so far two different methods: using fminsearch and csminwel ( I am aware of another option of csolve from Born & Pfeifer (2018). My model is a big scale model with 120 eqs.

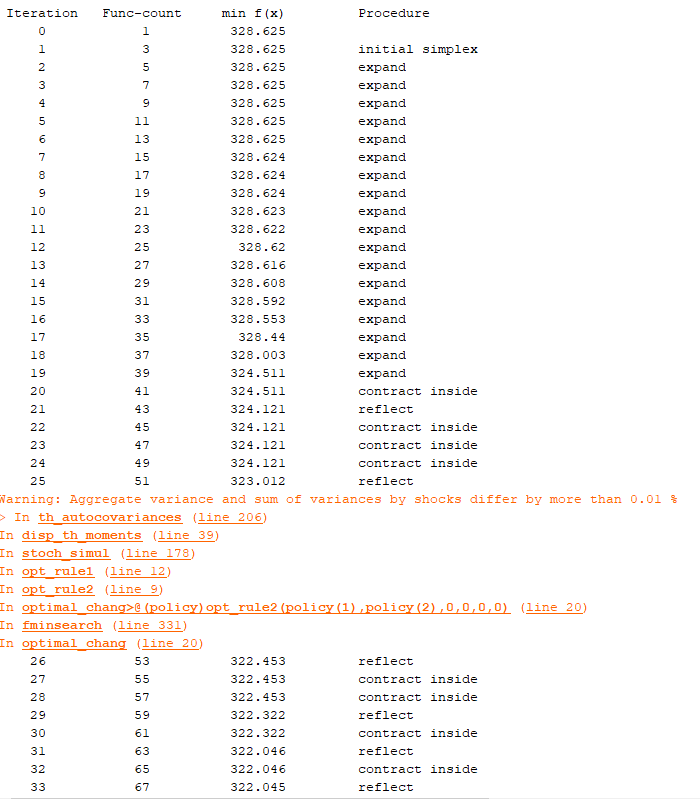
1. For fminsearch, my first run is to optimize only 2 params, the code work well using dynare 4.5 and matlab 2021a. However, from some point, the welfare value drops significantly and at the end reach a very small number (around zero) which suggest something wrong during optimization (I expect the changes in welfare value but not zero of -welfare). I attach the picture later. However, when I optimize with 4 parameters (2 in policy rule and 2 in tax rule), this does not happen and report reasonable results. Can anyone have any idea if something is wrong, or the algorithm problem or some models cannot be solved? Is there any way to set up the bound for params. I upload the code below but I cannot provide the mod file.
   

   

2. I tried with csminwel, following dynare forums, this is straightforward and the calculation time is much faster ( which may be a problem), I use dynare 4.6 for this run and the file in the attachment. My question is that the result seems to be extremely sensitive to initial point and the bound of params which raise the concern of accuracy, is there any way to improve this? Sometimes the algorithm failed to at some iterations also, is this because we go out of steady-state ?

3. I plan to optimize about 10 params, is it possible to do so (i know it may take really long time)? If it is possible, I am extremely grateful if someone can suggest more methods to do optimal analysis.

Thank you so much for everyone help.

optimal_rule_fminsearch.m (816 Bytes)
opimal_part.mod (541 Bytes)
welfare_objective.m (1.1 KB)

[jpfeifer]

A couple of points:

1. The cscolve in csolve from Born & Pfeifer (2018) is not an alternative. That one was used to compute the certainty equivalent for a given optimal policy, i.e. to solve an exact equation, not to minimize an objective.
2. It is well-known that local and global optimizers differ in their performance, see e.g.

Cmaes vs csminwel

csminwel is a Newton-type local optimizer. If you are close to the global mode, it will quickly converge to this this mode. But it can also converge to a local mode, i.e. fail to find the global one because it is local. cmaes is a global optimizer. It will be slower but has a higher likelihood of finding the global mode instead of just a local one.

Local optimizers will often depend on the starting point as they converge to the next local optimum.
3. As csminwel uses derivatives, it will typically show quadratic convergence and will be fast, but that comes with the downside of being local.
4. It is also well-known that loss functions tend to become very flat for large parameter values, so that bounds should be imposed. See e.g. A question about OSR command and policy frontier
5. The jump you describe above is not visible in the screenshot, but may indicate a large problem. Without the files it is impossible to tell.

[alexfra1709]

Dear Prof Pfeifer,
Thank you so much for your comment. It gives me some directions to move on. Look like I will try to do with what I have in my hand.