Observation mapping and different frequency handling

Estimation ML/Bayesian estimation
1

Dear Community,

I developed a model to check the impact of fiscal deficits and current account deficit on inflation. My model has 2 AR1 shock process: one for fiscal deficit and the other for current account deficit.

d = (1 - rho_d) * d_bar + rho_d * d(-1) + e_d;
yF = (1 - rho_yF) * yF_bar + rho_yF * yF(-1) + e_yF;

Where d and yF are the fiscal and current account deficit respectively as a percentage of GDP.

I read the “A Guide to Specifying Observation Equations for the Estimation of DSGE Models” by Johannes Pfeifer and I have encountered with 2 questions:

1- My model is at a monthly level, I have all my parameters and other observables at this frequency. The problem here is that fiscal and current account deficit data are yearly so what I did is to follow section 7.3 of the above mentioned guide and prepare the excel file accordingly, here is an extract of input data:

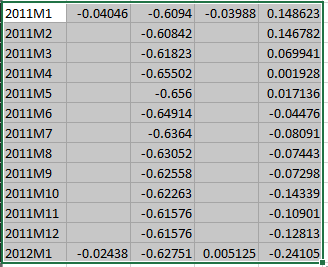
image

My question will be on how to map this to the model: What I understand from other questions from this forum is that deficit is a stock variable and output is a flow variable, so the data point is actually the level of deficit at that month, would this mean that the mapping of observable variable to the variable model is just:

d = d_obs;

2- My second question is related to: one, my shocks are AR1, so they are already linear, and two, because I am working with deficits, my data has negative numbers so I can’t log-linearized variables d and yF. So, how should I deal with the observation data? should I demean it around the steady state? or don’t do any transformations?

I did the first approach but I am not 100% sure if this is okay. Any advice will be such a help!

Thanks in advance!

Gustavo Pinto

2
  1. A deficit is not a stock, it’s a flow variable. It’s the outflow of the asset stock during a time period. Thus, the annual deficit is the sum of the monthly deficits. Your observation equation needs to reflect that.
  2. Your mapping in the data and in the model needs to be consistent. Your equations for d and yF imply that the variables have a non-zero mean. You need to deal with that. Similarly, you need to make sure the scaling and trend are consistent.