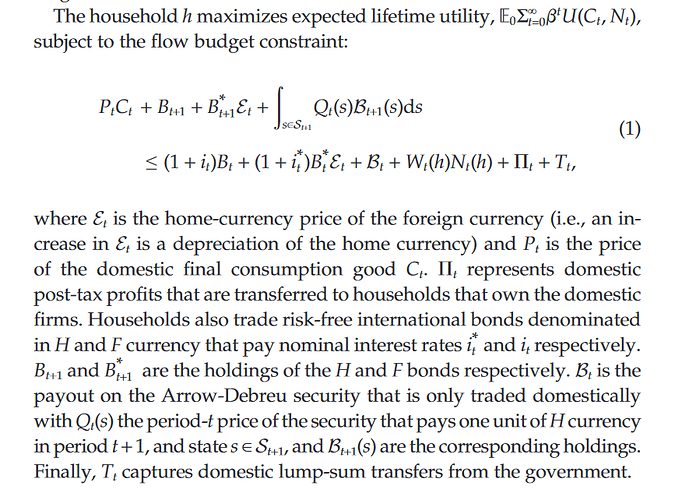Model with government bond (one and two economies)

General DSGE Modeling
1

Hello all,

I have a simple model based on Leeper. The model runs and it produces the IRFs that I expected it to produce. There is no residual and I have derived the analytical steady states.

var c n k z r w y q b g g_shock tau_k tau_l t t_shock;
varexo e_z e_g e_t;
parameters beta theta delta rho a psi psi_g g_ss b_ss tau_k_ss tau_l_ss;

beta = 0.99;
delta = 0.025;
theta = 0.36;
a = 1.72;
rho = 0.95;
psi = .25;
psi_g = .15;
g_ss = 0.0922;
b_ss = 0.3396;
tau_k_ss = 0.184;
tau_l_ss = 0.223;

steady_state_model;
z = 0;
t_shock = 0;
g_shock = 0;

tau_k = tau_k_ss;
tau_l = tau_l_ss;

r = (1 / (beta * (1 - tau_k_ss))) + delta - 1;
q = beta;
n = 1 / (1 + a * ((1 - g_ss)/((1 - tau_l_ss) * (1 - theta)) - (delta * theta)/((1 - tau_l_ss) * (1 - theta) * r)));
k = (r/(theta * n^(1 - theta)))^(1/(theta - 1));
w = (1 - theta) * k^(theta) * n^(-theta);
y = k^(theta) * n^(1 - theta);
g = g_ss * y;
c = y - delta * k - g;
b = b_ss * y;
t = tau_l * w * n + tau_k * r * k + q * b - b - g;
end;

model;
// First order conditions for households.
(((1 - tau_l) * w) / c)  = a / (1 - n);
beta * ((1/c(+1)) * (1 - tau_k(+1)) * (r(+1) + 1 - delta)) = (1 / c);
beta * (1/c(+1)) = (q / c);

// Household budget constraints.
c + k + q * b = (1 - tau_l) * w * n + (1 - tau_k) * r * k(-1) + (1 - delta) * k(-1) + b(-1) + t;

// Firm production.
y = exp(z) * k(-1)^(theta) * n^(1 - theta);
w = (1 - theta) * exp(z) * k(-1)^(theta) * n^(-theta);
r = theta * exp(z) * k(-1)^(theta - 1) * n^(1 - theta);

z = rho*(z(-1)) + e_z;

// Government budget constraint.
tau_l * w * n + tau_k * r * k(-1) + q * b = b(-1) + g + t;

// Government rules
log(t / steady_state(t)) = - psi * log((b / steady_state(b))) - psi_g * log((y/steady_state(y)))+ t_shock;
log(g / steady_state(g)) = - psi * log((b / steady_state(b))) - psi_g * log((y/steady_state(y))) + g_shock;
log(tau_l / steady_state(tau_l)) = psi * log((b / steady_state(b))) + psi_g * log((y/steady_state(y)));
log(tau_k / steady_state(tau_k)) = psi * log((b / steady_state(b))) + psi_g * log((y/steady_state(y)));

// Gov shocks
t_shock = rho*(t_shock(-1)) + e_t;
g_shock = rho*(g_shock(-1)) + e_g;

end;

model_diagnostics;
steady;
resid;

shocks;
var e_z = 0.01^2;
var e_t = 0.01^2;
var e_g = 0.01^2;


end;

stoch_simul(periods=2000, drop=200,irf = 100,order=1);//, replic=10000);

I extended the model into a two country model. Everything else is the same. I derived the analytical steady state and there is no residual, but I am getting the error of “Blanchard & Kahn conditions are not satisfied: no stable equilibrium.”

It is basically the same model, with almost the same analytical steady state.

var c_1 c_2 n_1 n_2 k_1 k_2 z_1 z_2 r_1 r_2 w_1 w_2 y_1 y_2 b_1 b_2 b_1_1 b_1_2 b_2_2 b_2_1 q_1 q_2 sigma_1 sigma_2 tau_n_1 tau_k_1 g_1 tau_n_2 tau_k_2 g_2 g_shock_1 g_shock_2 T_1 T_2 T_shock_1 T_shock_2;
varexo e_z_1 e_z_2 e_sigma_1 e_sigma_2 e_g_1 e_g_2 e_t_1 e_t_2;
parameters beta theta delta rho rhostar a pac omega omegastar b_1_2_bar b_2_1_bar psi psi_g tau_k_1_ss tau_n_1_ss tau_k_2_ss tau_n_2_ss g_1_ss g_2_ss b_1_ss b_2_ss;

beta = 0.99;
delta = 0.025;
theta = 0.36;
a = 1.72;
rho = 0.95;
rhostar = 0.95;
pac = 0.00074;
omega = 0.98;
b_1_2_bar = 0;
b_2_1_bar = 0;
omegastar = 0.98;
psi = 0.25;
psi_g = 0.15;
tau_k_1_ss = 0.184;
tau_n_1_ss = 0.223;
tau_k_2_ss = 0.184;
tau_n_2_ss = 0.223;
g_1_ss = 0.0922;
g_2_ss = 0.0922;
b_1_ss = 0.3396;
b_2_ss = 0.3396;

steady_state_model;
z_1 = 0;
sigma_1 = 0;

T_shock_1 = 0;
g_shock_1 = 0;

tau_k_1 = tau_k_1_ss;
tau_n_1 = tau_n_1_ss;

r_1 = (1 / (beta * (1 - tau_k_1))) + delta - 1;
q_1 = beta;
n_1 = 1 / (1 + a * ((1 - g_1_ss)/((1 - tau_n_1) * (1 - theta)) - (delta * theta)/((1 - tau_n_1) * (1 - theta) * r_1)));
k_1 = (r_1/(theta * n_1^(1 - theta)))^(1/(theta - 1));
w_1 = (1 - theta) * k_1^(theta) * n_1^(-theta);
y_1 = k_1^(theta) * n_1^(1 - theta);
g_1 = g_1_ss * y_1;
c_1 = y_1 - delta * k_1 - g_1;
b_1 = b_1_ss * y_1;
T_1 = tau_n_1 * w_1 * n_1 + tau_k_1 * r_1 * k_1 + q_1 * b_1 - b_1 - g_1;
b_1_1 = b_1;
b_1_2 = 0;

z_2 = 0;
sigma_2 = 0;

T_shock_2 = 0;
g_shock_2 = 0;

tau_k_2 = tau_k_2_ss;
tau_n_2 = tau_n_2_ss;

r_2 = (1 / (beta * (1 - tau_k_2))) + delta - 1;
q_2 = beta;
n_2 = 1 / (1 + a * ((1 - g_2_ss)/((1 - tau_n_2) * (1 - theta)) - (delta * theta)/((1 - tau_n_2) * (1 - theta) * r_2)));
k_2 = (r_2/(theta * n_2^(1 - theta)))^(1/(theta - 1));
w_2 = (1 - theta) * k_2^(theta) * n_2^(-theta);
y_2 = k_2^(theta) * n_2^(1 - theta);
g_2 = g_2_ss * y_2;
c_2 = y_2 - delta * k_2 - g_2;
b_2 = b_2_ss * y_2;
T_2 = tau_n_2 * w_2 * n_2 + tau_k_2 * r_2 * k_2 + q_2 * b_2 - b_2 - g_2;
b_2_1 = 0;
b_2_2 = b_2;

end;

model;
/*
Home Economy - Denoted by country 1
*/
y_1 = exp(z_1) * k_1(-1)^theta * n_1^(1 - theta);

/*
Constraints for home Economy
*/
c_1 + k_1 + q_1 * b_1_1 + q_2 * b_1_2 + 0.5 * pac * (b_1_2 - b_1_2_bar)^2 = (1 - tau_n_1) * w_1 * n_1 + (1 - tau_k_1) * r_1 * k_1(-1) + (1 - delta) * k_1(-1) + b_1_1(-1) + b_1_2(-1) + T_1;

/*
FOC - intra temporal, capital accumulation, and bond accumulation
*/
a / (1 - n_1) = (w_1 / c_1) * (1 - tau_n_1);
1 / c_1 = beta * ((1 / c_1(+1)) * (1 - tau_k_1(+1)) * (r_1(+1) + 1 - delta));
beta * (1 /c_1(+1)) = ((q_2 + pac * (b_1_2 - b_1_2_bar)) / c_1);
beta * (1 /c_1(+1)) = (q_1 / c_1);

/*
Prices
*/
r_1 = theta * exp(z_1) * k_1(-1)^(theta - 1) * n_1^(1-theta);
w_1 = (1 - theta) * exp(z_1) * k_1(-1)^(theta) * n_1^(-theta);

/*
TFP
*/
z_1 = rho * z_1(-1) + exp(sigma_1) * e_z_1;
sigma_1 = omega * sigma_1(-1) + e_sigma_1;

/*
Government of country 1 BC
*/
tau_n_1 * w_1 * n_1 + tau_k_1 * r_1 * k_1(-1) + q_1 * b_1 = b_1(-1) + g_1 + T_1;


// Government rules
log(T_1 / steady_state(T_1)) = - psi * log((b_1 / steady_state(b_1))) - psi_g * log((y_1/steady_state(y_1))) + T_shock_1;
log(g_1 / steady_state(g_1)) = - psi * log((b_1 / steady_state(b_1))) - psi_g * log((y_1/steady_state(y_1))) + g_shock_1;
log(tau_n_1 / steady_state(tau_n_1)) = psi * log((b_1 / steady_state(b_1))) + psi_g * log((y_1/steady_state(y_1)));
log(tau_k_1 / steady_state(tau_k_1)) = psi * log((b_1 / steady_state(b_1))) + psi_g * log((y_1/steady_state(y_1)));

// Gov shocks
T_shock_1 = rho*(T_shock_1(-1)) + e_t_1;
g_shock_1 = rho*(g_shock_1(-1)) + e_g_1;

/*
Foreign Economy denoted by country 2
*/
y_2 = exp(z_2) * k_2(-1)^theta * n_2^(1 - theta);

/*
Constraints for foreign Economy
*/
c_2 + k_2 + q_2 * b_2_2 + q_1 * b_2_1 + 0.5 * pac * (b_2_1 - b_2_1_bar)^2 = (1 - tau_n_2) * w_2 * n_2 + (1 - tau_k_2) * r_2 * k_2(-1) + (1 - delta) * k_2(-1) + b_2_2(-1) + b_2_1(-1) + T_2;

/*
FOC - intra temporal, capital accumulation, and bond accumulation
*/
a / (1 - n_2) = (w_2 / c_2) * (1 - tau_n_2);
1 / c_2 = beta * ((1 / c_2(+1)) * (1 - tau_k_2(+1)) * (r_2(+1) + 1 - delta)) ;
beta * (1 /c_2(+1)) = ((q_1 + pac * (b_2_1 - b_2_1_bar)) / c_2);
beta * (1 /c_2(+1)) = (q_2 / c_2);

/*
Prices
*/
r_2 = theta * exp(z_2) * k_2(-1)^(theta - 1) * n_2^(1-theta);
w_2= (1 - theta) * exp(z_2) * k_2(-1)^(theta) * n_2^(-theta);

/*
TFP
*/
z_2 = rho * z_2(-1) + exp(sigma_2) * e_z_2;
sigma_2 = omega * sigma_2(-1) + e_sigma_2;

/*
Government of country 2 BC
*/
tau_n_2 * w_2 * n_2 + tau_k_2 * r_2 * k_2(-1) + q_2 * b_2 = b_2(-1) + g_2 + T_2;


// Government rules
log(T_2 / steady_state(T_2)) = - psi * log((b_2 / steady_state(b_2))) - psi_g * log((y_2/steady_state(y_2))) + T_shock_2;
log(g_2 / steady_state(g_2)) = - psi * log((b_2 / steady_state(b_2))) - psi_g * log((y_2/steady_state(y_2))) + g_shock_2;
log(tau_n_2 / steady_state(tau_n_2)) = psi * log((b_2 / steady_state(b_2))) + psi_g * log((y_2/steady_state(y_2)));
log(tau_k_2 / steady_state(tau_k_2)) = psi * log((b_2 / steady_state(b_2))) + psi_g * log((y_2/steady_state(y_2)));

// Gov shocks
T_shock_2 = rho*(T_shock_2(-1)) + e_t_2;
g_shock_2 = rho*(g_shock_2(-1)) + e_g_2;

/*
Bond market clearing
*/
b_1 = b_1_1 + b_2_1;
b_2 = b_2_2 + b_1_2;

end;

model_diagnostics;
steady;
resid;

shocks;
var e_z_1 = 0.01^2;
var e_t_1 = 0.01^2;
var e_g_1 = 0.01^2;

var e_z_2 = 0.01^2;
var e_t_2 = 0.01^2;
var e_g_2 = 0.01^2;

end;

stoch_simul(periods=2000, drop=200,irf = 100,order=1);

Can anyone point to what might be the problem? I have a feeling that it has something to do with international bonds - but I used a portfolio adjustment cost as suggested by Schmidt-Grohe.

Does home household buying home bond also need to have portfolio adjustment cost? Because right now, I only put the cost when they hold international bonds.

Thanks!

2

I browsed your codes. It seems that the numbers of equations of both countries are same. My very immature thought follows:

If adding all constraints of entities in country H, we will conclude a so-called current account / balance of payment equation. However, this is exactly the reverse of the current account equation of country F. So for the country F side, the total number of equations is one less.

From the perspective of H, we can obtain FOCs wrt B_{Ht} and B_{Ft}; and from the angle of F, we will have FOCs wrt B_{Ht}^* and B_{Ft}^*. In one book, the author said: considering the bond market clearing conditions, there is one redundant equation among these four, i.e., three FOCs can recover the rest one. But I never check this claim. Just for your reference.

3

I agree that the two bond market clearing conditions look strange.

4

I don’t think I understand.

Country 1 household decides on how much of the foreign bond it would own.
Country 2 household decides on how much of the domestic bond it would own.

Add these together, you have bond demand. Demand from foreign country, and demand from domestic household. Demand should equal to supply, with q the market clearing price.

Same thing with the opposite of that.

If I remove any of the FOC, I am saying that that country household doesn’t decide on how much bond it demands, which makes no sense.

5

I don’t think I understand.

Country 1 household decides on how much of the foreign bond it would own.
Country 2 household decides on how much of the domestic bond it would own.

Add these together, you have bond demand. Demand from foreign country, and demand from domestic household. Demand should equal to supply, with q the market clearing price.

Same thing with the opposite of that.

If I remove any of the FOC, I am saying that that country household doesn’t decide on how much bond it demands, which makes no sense.

6

@jpfeifer

@HelloDynare

I think what I am trying to do here is not possible - you can’t have 2 assets traded internationally. You can have only one internationally traded asset. At least that’s what Mendoza and Tesar (1998) and Fogli and Perri (2015) said.

7

Hi @swooneytoad,

I’m happy receiving your response :slightly_smiling_face:

I ran model_diagnostics(M_, options_, oo_) in MATLAB command window (version: Dynare 4.6.4).

MODEL_DIAGNOSTICS:  The Jacobian of the static model is singular
MODEL_DIAGNOSTICS:  there is 8 colinear relationships between the variables and the equations

Relation 1
Colinear variables:
c_2 n_1 n_2 k_1 k_2 r_1 r_2 w_1 w_2 y_1 y_2
b_1 b_2 b_1_1 b_2_2 tau_n_1 tau_k_1 g_1
tau_n_2 tau_k_2 g_2 T_1 T_2
Relation 2
Colinear variables:
c_2 n_1 n_2 k_1 k_2 r_1 r_2 w_1 w_2 y_1 y_2
b_1 b_2 b_1_1 b_2_2 tau_n_1 tau_k_1 g_1
tau_n_2 tau_k_2 g_2 T_1 T_2
Relation 3
Colinear variables:
c_2 n_1 n_2 k_1 k_2 r_1 r_2 w_1 w_2 y_1 y_2
b_1 b_2 b_1_1 b_2_2 tau_n_1 tau_k_1 g_1
tau_n_2 tau_k_2 g_2 T_1 T_2
Relation 4
Colinear variables:
c_2 n_1 n_2 k_1 k_2 r_1 r_2 w_1 w_2 y_1 y_2
b_1 b_2 b_1_1 b_2_2 tau_n_1 tau_k_1 g_1 
tau_n_2 tau_k_2 g_2 T_1 T_2
Relation 5
Colinear variables:
c_2 n_1 n_2 k_1 k_2 r_1 r_2 w_1 w_2 y_1 y_2
b_1 b_2 b_1_1 b_2_2 tau_n_1 tau_k_1 g_1
tau_n_2 tau_k_2 g_2 T_1 T_2
Relation 6
Colinear variables:
c_2 n_1 n_2 k_1 k_2 r_1 r_2 w_1 w_2 y_1 y_2
b_1 b_2 b_1_1 b_2_2 tau_n_1 tau_k_1 g_1
tau_n_2 tau_k_2 g_2 T_1 T_2
Relation 7
Colinear variables:
c_2 n_1 n_2 k_1 k_2 r_1 r_2 w_1 w_2 y_1 y_2
b_1 b_2 b_1_1 b_2_2 tau_n_1 tau_k_1 g_1
tau_n_2 tau_k_2 g_2 T_1 T_2
Relation 8
Colinear variables:
c_1 n_1 k_1 r_1 w_1 y_1 b_1 b_1_1
tau_n_1 tau_k_1 g_1 T_1

Relation 1
Colinear equations
    12    13    14    15    16    17
Relation 2
Colinear equations
    12    13    14    15    16    17

Relation 3
Colinear equations
    29    30    31    33    34

Relation 4
Colinear equations
    29    30    31    33    34

Relation 5
Colinear equations
    32

Relation 6
Colinear equations
    12    13    14    15    16    17

Relation 7
Colinear equations
    12    13    14    15    16    17

Relation 8
Colinear equations
    29    30    31    33    34

MODEL_DIAGNOSTICS:  The presence of a singularity problem typically indicates that there is one
MODEL_DIAGNOSTICS:  redundant equation entered in the model block, while another non-redundant equation
MODEL_DIAGNOSTICS:  is missing. The problem often derives from Walras Law.
8

I partially agree with your concern. In the code,

/*
Constraints for home Economy
*/
c_1 + k_1 + q_1 * b_1_1 + q_2 * b_1_2 + 0.5 * pac * (b_1_2 - b_1_2_bar)^2 = (1 - tau_n_1) * w_1 * n_1 + (1 - tau_k_1) * r_1 * k_1(-1) + (1 - delta) * k_1(-1) + b_1_1(-1) + b_1_2(-1) + T_1;

/*
Constraints for foreign Economy
*/
c_2 + k_2 + q_2 * b_2_2 + q_1 * b_2_1 + 0.5 * pac * (b_2_1 - b_2_1_bar)^2 = (1 - tau_n_2) * w_2 * n_2 + (1 - tau_k_2) * r_2 * k_2(-1) + (1 - delta) * k_2(-1) + b_2_2(-1) + b_2_1(-1) + T_2;

b_1_1 and b_1_2, b_2_2 and b_2_1 are so identical with each other, such that I doubt the computer may determine them jointly, but cannot figure out each of them individually. The SGU adjustment cost alleviates this worry. Dynare said the key problem is the violation of Walras Law.

But I definitely saw some papers that allow “2 assets traded internationally”.
For example, (and again,) in the paper
The Macroeconomics of Border Taxes

Screenshot_HouseholdsBGT
Screenshot_HouseholdsBGT876×642 106 KB

Both B_{t+1} and B_{t+1}^* are international bonds, though they are denominated in H and F currency respectively. The Arrow security \mathcal{B}_{t+1} is purely traded domestically.

(I’m not an expert in macro modelling, please feel free to share your views :speech_balloon:)

9

Your model shows explosiveness. That may be due to the fiscal rules not stabilizing debt. Have you tried whether the model works with different fiscal rules. At the moment, you restrict all feedback to be the same across countries and instruments.

10

There is an indeterminacy problem here.

In the steady state - the amount of debt issued by the government is a parameter (b_ss*y) and that is a known number, as long as we know what y is.

But, the debt holding is not fixed - it can be in any combination;
b_1_1 + b_2_1 = steady_state debt

b_1_1 can be 0 and b_2_1 = ss debt.
b_2_1 can be 0 and b_1_1 = ss debt.

Or any number, actually. I think this is the main problem with. There is an infinite steady state.