Model consistent paths to the steady-state

Perfect foresight simulations
1

Dear all,

Just a quick clarification. If a start a perfect foresight simulation from a point different from the steady-state, and include only a few periods (say 20), I should observe a path model consistent in the entire 20 + 2 (initial + final period), right?

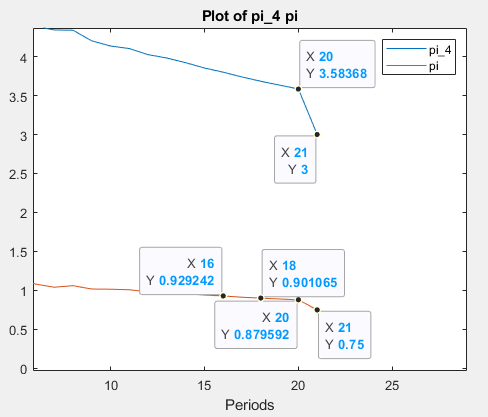
For example, the variable \pi^4_t = \pi_t + \pi_{t-1} + \pi_{t-2} + \pi_{t-3} should get to the steady-state ( = 3 in this example) at t = 21 (end value), with \pi_{20}, \pi_{19}, \pi_{18} consistent with \pi_{21} also at the steady-state (= 0.75).

The figures below illustrates that this does not happen, as \pi^4_{21} = 0.75+0.90+0.88+0.93 > 3. Feels like he is not taking into account correctly the number of periods and/or end-values.

image

Thanks in advance !

2
  1. If the process is purely backward-looking, then the terminal condition will not matter. \pi_{21} is not endogenously computed and will not matter.
  2. As a general rule, your model needs sufficient time to converge to the terminal steady state.
3

Thanks for your reply @jpfeifer

  1. Although \pi^4_t is purely backward looking, \pi_t is a forward looking variable. Does that mean that terminal conditions won’t matter for \pi^4_t but matter for \pi_t?

  2. If I use the command:

endval;

pi = 1.00

end:

Before the perfect_foresight_setup command, theoretically, should I see \pi_t converging to 1.00 instead of 0.75 (original steady-state value) in oo_.endo_simul ?

  1. If periods are not sufficient for convergence, shouldn’t I see a problem in the optimization routine ? Because, from the mathematical point of view, the two boundary value problem is well defined given any amount of periods and initial / terminal conditions.

Thanks again in advance !

4
  1. In that case, the terminal condition will only indirectly matter for \pi_t^4 via its effect on \pi_t.
  2. Yes, that is the point of endval. However, terminal conditions usually only make sense if you have a steady state as the terminal condition.
  3. Yes, the mathematical two boundary problem is still well-defined. The economic problem often is not, because the terminal condition of being in steady state will be incorrect if there is insufficient time for the problem to settle back to steady state. You can often see this issue by abrupt jumps in the last period, which are fine mathematically but not economically.
1 Like
5

Many thanks professor !