In Ramsey’s optimal policy, low price stickiness results in low inflation volatility and low output gap volatility. Thus, firms choose prices every quarter (\frac{1}{1-\theta} \approx1,\;\; \theta \rightarrow 0), but almost the same price every quarter?
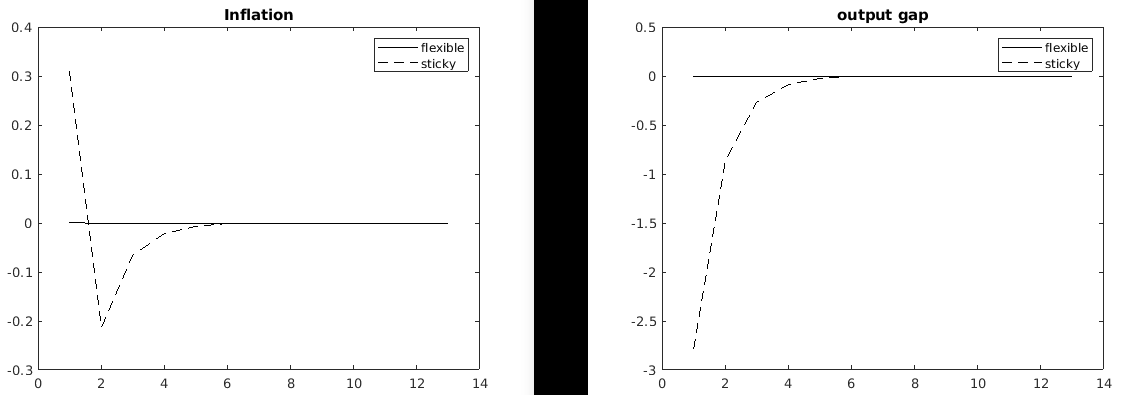
In the plots above, \theta \rightarrow 0 (flexible, but not fully flexible), \theta \rightarrow 1 (sticky, but not fully sticky). \theta is calvo parameter.
Sorry, but I don’t understand the question.
Like in Gali (2015), Ch5, if you reduce the Calvo parameter from 0.75 in the book to say 0.001, you get low volatility of the inflation rate and output gap (almost zero) - what I have named ‘flexible’ in the plots. But a low Calvo parameter also means low price stickiness and shorter duration of price change.
I am trying to link the two. Thus, if Calvo parameter (\theta) \rightarrow 0,
How can that be? It seems firms choose their optimal price (p_t^* \approx u = some constant mark-up$) every quarter (\frac{1}{1-\theta}), yeah? So although the price does not change much, firms choose it every quarter.
If the Calvo parameter is 0, you are back to the classical monetary economy of Chapter 2. Prices are indeed a constant over marginal costs each period.