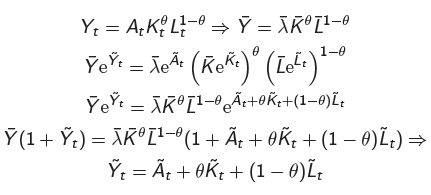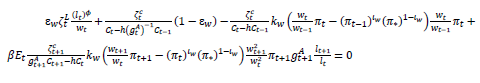Log-linearization of complex equations Uhlig’s method

Stochastic simulations
1

Dear all,
I need to log-linearize a large system of equations for bayesian estimation using the Uhlig’s method.
Will Dynare be able to evaluate the model if the equations are written in an intermediate form as in equation 4? Or only the final version.
P1
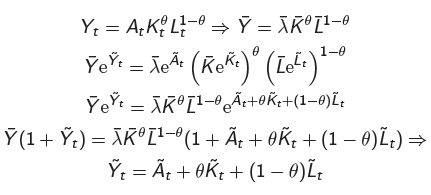
This is a big problem for me, ‘cause a more complex equation is quite difficult to solve (like this one):

P2
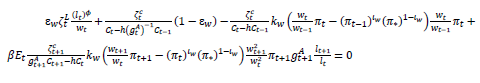
Perhaps you can advise a more effective way to solve this problem.

2

If you are using Dynare, why are you even linearizing by hand?

3

I want to get estimates of the a posteriori distribution of parameters of the term 1 model. However, I am faced with «ERROR: If the model is declared linear the second derivatives must be equal to zero. The following equations have non-zero second derivatives:…».

The authors of the term1 model use “Symbolic Toolbox” for log linearization of equations, however, I could not find any detailed information about this tool, except for “Automatic Solution and Log Linearization of DSGE Models” by Tom Holden. But Tom’s code couldn’t solve my problem.

term1 - initial model, term2 - transformed model.
term1.mod (24.4 KB)
term2.mod (23.6 KB)
StData.xlsx (21.4 KB)

4

Again, there is no reason to linearize by hand. Dynare can deal with the nonlinear equations.

5

Thank you very much, Johannes. I managed to solve my problem.
One short question: so for Dynare there is no difference between calculations of a logarithmically linearized model and a nonlinear one?

6

No. See also