Hi everyone,
Could anyone help me with this detailed derivation of Euler equation?
I’m not sure Log-linearizing of the following equation (1):
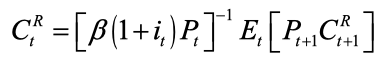
equal equation (2)
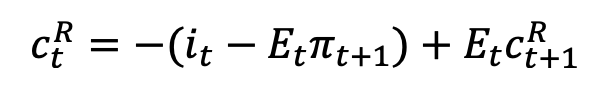
or equation (3)
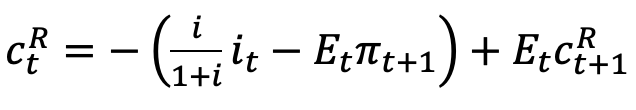
Thanks.
Hi everyone,
Could anyone help me with this detailed derivation of Euler equation?
I’m not sure Log-linearizing of the following equation (1):
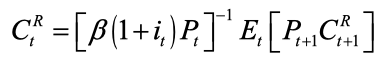
equal equation (2)
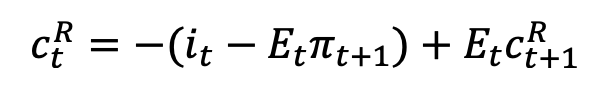
or equation (3)
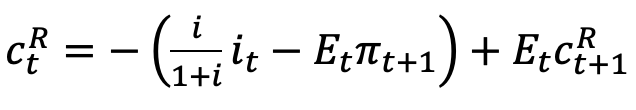
Thanks.
The relevant part is the Taylor approximation of \frac{1}{1+i} with respect to i, which is -\frac{1}{(1+i)^2}(i_t- i)=-\frac{i}{(1+i)^2}\frac{i_t-i}{i}=-\frac{i}{(1+i)^2}\hat i_t. After canceling the \frac{1}{1+i} term present in all terms of the equation, you are left with -\frac{i}{1+i}\hat i_t, which corresponds to (3).
You should get (2) if you are not interested in percentage deviations of the net interest rate i_t from its steady state, but of the gross interest rate 1+i_t from its steady state. But you did not explain the notation.
Hi Prof,
Thank you for your detailed explanation. In my question, i is the net interest rate. That’s why I’m so confused. If I care about the percentage deviations of the gross interest rate from its steady state. I should get the following equation, right?
Yes, indeed, but 1+i\approx 1, so the percentage deviation of the gross interest rate from its steady state is often approximated by the net interest rate deviation.